题目内容
椭圆| x2 | 4 |
分析:解法一:运用特值法,取M为椭圆右顶点(2,0),则x1=2,x2=2,由此可求出x1•x2的值.
解法二:设M(2cosθ,sinθ),直线B1M的方程为:
=
,令y=0,得x1=
,直线B2M的方程为:
=
,令y=0,得x2=
,由此可求出x1•x2的值.
解法二:设M(2cosθ,sinθ),直线B1M的方程为:
| y+1 |
| x |
| sinθ+1 |
| 2cosθ |
| 2cosθ |
| sinθ+1 |
| y-1 |
| x |
| sinθ-1 |
| 2cosθ |
| 2cosθ |
| 1-sinθ |
解答:解法一:取M为椭圆右顶点(2,0),则x1=2,x2=2,∴x1•x2=4.
解法二:由椭圆
+y2=1得
,θ为参数,设M(2cosθ,sinθ),
直线B1M的方程为:
=
,令y=0,得x1=
,
直线B2M的方程为:
=
,令y=0,得x2=
,
∴x1•x2=
•
=4.
答案:4.
解法二:由椭圆
| x2 |
| 4 |
|
直线B1M的方程为:
| y+1 |
| x |
| sinθ+1 |
| 2cosθ |
| 2cosθ |
| sinθ+1 |
直线B2M的方程为:
| y-1 |
| x |
| sinθ-1 |
| 2cosθ |
| 2cosθ |
| 1-sinθ |
∴x1•x2=
| 2cosθ |
| sinθ+1 |
| 2cosθ |
| 1-sinθ |
答案:4.
点评:特值法是求解选择题和填空题的有效方法.

练习册系列答案
相关题目
椭圆
+y2=1的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则P到F2的距离为( )
| x2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、4 |
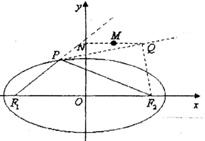 如图,已知椭圆
如图,已知椭圆