题目内容
抛物线y2=2x上的点P（x,y）到点A（a,0）(a∈R)的距离的最小值记为f（a）.（1）求f（a）的表达式；（2）当
≤a≤5时，求f（a）的最大值和最小值.
思路解析：利用两点间的距离公式构造目标函数，注意分类讨论.
解：（1）|PA|==
=
.
当a-1＜0，即a＜1时，f（a）=|a|；
当a-1≥0，即a≥1时，f（a）=
.
∴f（a）=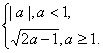
（2）当
≤a≤5时，
①若a∈［
，1
，f（a）=a在［
，1
上为增函数，
∴f（a）min=f（
）=
;
②若a∈［1，5］，f（a）=
在［1，5］上为增函数，
∴f（a）max=f（5）=
=3.
综上,知f（a）的最大值为3，最小值为
.
练习册系列答案
相关题目
若抛物线y2=2x上的一点到焦点的距离为5，则该点的坐标为（ ）
A、（4，2
| ||
| B、（5，10） | ||
| C、（4.5，3） | ||
D、（6，2
|
抛物线y2=2x上的点P到直线y=2x+4有最短的距离，则P的坐标是（ ）
A、（
| ||||
| B、（0，0） | ||||
| C、（2，2） | ||||
D、(
|
记定点M（3，
）与抛物线y2=2x上的动点P之间的距离为d1，P到抛物线准线的距离为d2，则d1+d2的最小值为（ ）
| 10 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|