题目内容
A={a+2，（a+1）2，a2+3a+3}，若1∈A，求a的值．
因为A={a+2，（a+1）2，a2+3a+3}，又1∈A，
所以当a+2=1时，解得a=-1，此时a2+3a+3=1，违背了集合中元素的互异性，所以舍去；
当（a+1）2=1时，解得a=0或a=-2，若a=0，集合A={2，1，3}，符合题意，若a=-2，此时（a+1）2=a2+3a+3=1，违背集合中元素的互异性，所以舍去；
当a2+3a+3=1时，解得a=-1或a=-2，均违背集合中元素的互异性．
所以所求a的值为0．
所以当a+2=1时，解得a=-1，此时a2+3a+3=1，违背了集合中元素的互异性，所以舍去；
当（a+1）2=1时，解得a=0或a=-2，若a=0，集合A={2，1，3}，符合题意，若a=-2，此时（a+1）2=a2+3a+3=1，违背集合中元素的互异性，所以舍去；
当a2+3a+3=1时，解得a=-1或a=-2，均违背集合中元素的互异性．
所以所求a的值为0．
练习册系列答案
相关题目
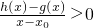在D内恒成立，则称P为函数y=h（x）的“类对称点”，请你探究当a=4时，函数y=f（x）是否存在“类对称点”，若存在，请最少求出一个“类对称点”的横坐标；若不存在，说明理由．
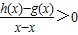在D内恒成立，则称P为函数y=h（x）的“类对称点”，请你探究当a=4时，函数y=f（x）是否存在“类对称点”，若存在，请最少求出一个“类对称点”的横坐标；若不存在，说明理由．
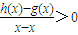在D内恒成立，则称P为函数y=h（x）的“类对称点”，请你探究当a=4时，函数y=f（x）是否存在“类对称点”，若存在，请最少求出一个“类对称点”的横坐标；若不存在，说明理由．