��Ŀ����
��֪����f��x��=x2-��a+2��x+alnx�����г���a��0����1����a��2ʱ������f��x���ĵ����������䣻
��2����a=4ʱ��������y=f��x��-m��������ͬ����㣬��m��ȡֵ��Χ��
��3���趨����D�ϵĺ���y=h��x���ڵ�p��x��h��x�����������߷���Ϊl��y=g��x������x��xʱ����
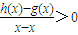 ��D�ں���������PΪ����y=h��x���ġ���ԳƵ㡱������̽����a=4ʱ������y=f��x���Ƿ���ڡ���ԳƵ㡱�������ڣ����������һ������ԳƵ㡱�ĺ����ꣻ�������ڣ�˵�����ɣ�
��D�ں���������PΪ����y=h��x���ġ���ԳƵ㡱������̽����a=4ʱ������y=f��x���Ƿ���ڡ���ԳƵ㡱�������ڣ����������һ������ԳƵ㡱�ĺ����ꣻ�������ڣ�˵�����ɣ�
���𰸡���������1��f�䣨x��=2x-��a+2��+ =
= ����f����x����0�����f��x���ĵ����������䣻
����f����x����0�����f��x���ĵ����������䣻
��2����a=4ʱ��f��x��=x2-6x+4lnx��f�䣨x��=2x+ -6������x��0����f����x��=0�����ֵ�㣬�Ѻ���y=f��x��-m��������ͬ�����ת��Ϊ����y=f��x����ͼ����ֱ��y=m�Ľ�����������
-6������x��0����f����x��=0�����ֵ�㣬�Ѻ���y=f��x��-m��������ͬ�����ת��Ϊ����y=f��x����ͼ����ֱ��y=m�Ľ�����������
��3����a=4ʱ������y=f��x������ͼ����һ��P��x��f��x�����������߷���Ϊy=m��x��=
 ���ɴ����Ƶ���y=f��x�����ڡ���ԳƵ㡱��
���ɴ����Ƶ���y=f��x�����ڡ���ԳƵ㡱�� ��һ������ԳƵ㡱�ĺ����꣮
��һ������ԳƵ㡱�ĺ����꣮
����⣺��1����f��x��=x2-��a+2��x+alnx��
��f�䣨x��=2x-��a+2�� =
= ������x��0��
������x��0��
��f'��x��=0����x=1��x= ��
��
��a��2���� ��1��
��1��
��0��x��1��x�� ʱ��f'��x����0��
ʱ��f'��x����0��
��1��x�� ʱ��f'��x����0��
ʱ��f'��x����0��
��f��x���ĵ�����������Ϊ��0��1������ ��+�ޣ���
��+�ޣ���
��2����a=4ʱ��f��x��=x2-6x+4lnx��f�䣨x��=2x+ -6=
-6= =
= ������x��0��
������x��0��
��x�ʣ�0��1������2��+�ޣ�ʱ��f����x����0��
��x�ʣ�1��2��ʱ��f����x����0��
��f��x����x�ʣ�0��1������2��+�ޣ�ʱΪ��������
��x�ʣ�1��2��ʱΪ��������
��f��x���ļ���ֵΪf��1��=-5����СֵΪf��2��=4ln2-8��
Ҫʹ����y=f��x��-m��������ͬ����㣬������y=f��x����ͼ����ֱ��y=m��������ͬ���㣬
��ͼ����m��ȡֵ��Χ�ǣ�4ln2-8��-5����
��3���ɣ�2��֪����a=4ʱ������y=f��x������ͼ����һ��P��x��f��x�����������߷���Ϊ��
y=m��x��= ��
��
��գ�x��=f��x��-m��x��= ��
��
��գ�x��=0��
ϕ�䣨x��=2x+ -6-��2x+
-6-��2x+ -6��=2��x-x����1-
-6��=2��x-x����1- ��=
��= ��x-x����x-
��x-x����x- ��
��
��x�� ���գ�x���ڣ�x��
���գ�x���ڣ�x�� ���ϵ����ݼ���
���ϵ����ݼ���
�൱x�ʣ�x�� ��ʱ���գ�x�����գ�x��=0����ʱ
��ʱ���գ�x�����գ�x��=0����ʱ ��0��
��0��
�� ���գ�x���ڣ�
���գ�x���ڣ� ��x���ϵ����ݼ���
��x���ϵ����ݼ���
�൱x�ʣ� ��x��ʱ���գ�x�����գ�x��=0����ʱ
��x��ʱ���գ�x�����գ�x��=0����ʱ ��0��
��0��
��y=f��x���ڣ�0�� ���ȣ�
���ȣ� ��+�ޣ��ϲ����ڡ���ԳƵ㡱��
��+�ޣ��ϲ����ڡ���ԳƵ㡱��
�� ��
�� ��0��
��0��
��գ�x���ڣ�0��+�ޣ�������������
��x��xʱ���գ�x�����գ�x��=0��
��x��xʱ���գ�x�����գ�x��=0���� ��0��
��0��
����ʱ��P��y=f��x���ġ���ԳƵ㡱
���ϣ�y=f��x�����ڡ���ԳƵ㡱�� ��һ������ԳƵ㡱�ĺ����꣮
��һ������ԳƵ㡱�ĺ����꣮
���������⿼�麯���ĵ������������̽�����㺯����һ������µIJ�������̽�������Ƿ���ڡ���ԳƵ㡱������ʱҪ�������⣬ע���������˼��͵ȼ�ת��˼��ĺ������ã����������⣮
 =
= ����f����x����0�����f��x���ĵ����������䣻
����f����x����0�����f��x���ĵ����������䣻��2����a=4ʱ��f��x��=x2-6x+4lnx��f�䣨x��=2x+
 -6������x��0����f����x��=0�����ֵ�㣬�Ѻ���y=f��x��-m��������ͬ�����ת��Ϊ����y=f��x����ͼ����ֱ��y=m�Ľ�����������
-6������x��0����f����x��=0�����ֵ�㣬�Ѻ���y=f��x��-m��������ͬ�����ת��Ϊ����y=f��x����ͼ����ֱ��y=m�Ľ�������������3����a=4ʱ������y=f��x������ͼ����һ��P��x��f��x�����������߷���Ϊy=m��x��=

 ���ɴ����Ƶ���y=f��x�����ڡ���ԳƵ㡱��
���ɴ����Ƶ���y=f��x�����ڡ���ԳƵ㡱�� ��һ������ԳƵ㡱�ĺ����꣮
��һ������ԳƵ㡱�ĺ����꣮����⣺��1����f��x��=x2-��a+2��x+alnx��
��f�䣨x��=2x-��a+2��
 =
= ������x��0��
������x��0����f'��x��=0����x=1��x=
 ��
����a��2����
 ��1��
��1����0��x��1��x��
 ʱ��f'��x����0��
ʱ��f'��x����0����1��x��
 ʱ��f'��x����0��
ʱ��f'��x����0����f��x���ĵ�����������Ϊ��0��1������
 ��+�ޣ���
��+�ޣ�����2����a=4ʱ��f��x��=x2-6x+4lnx��f�䣨x��=2x+
 -6=
-6= =
= ������x��0��
������x��0����x�ʣ�0��1������2��+�ޣ�ʱ��f����x����0��
��x�ʣ�1��2��ʱ��f����x����0��
��f��x����x�ʣ�0��1������2��+�ޣ�ʱΪ��������
��x�ʣ�1��2��ʱΪ��������
��f��x���ļ���ֵΪf��1��=-5����СֵΪf��2��=4ln2-8��
Ҫʹ����y=f��x��-m��������ͬ����㣬������y=f��x����ͼ����ֱ��y=m��������ͬ���㣬
��ͼ����m��ȡֵ��Χ�ǣ�4ln2-8��-5����
��3���ɣ�2��֪����a=4ʱ������y=f��x������ͼ����һ��P��x��f��x�����������߷���Ϊ��
y=m��x��=
 ��
����գ�x��=f��x��-m��x��=
 ��
����գ�x��=0��
ϕ�䣨x��=2x+
 -6-��2x+
-6-��2x+ -6��=2��x-x����1-
-6��=2��x-x����1- ��=
��= ��x-x����x-
��x-x����x- ��
����x��
 ���գ�x���ڣ�x��
���գ�x���ڣ�x�� ���ϵ����ݼ���
���ϵ����ݼ����൱x�ʣ�x��
 ��ʱ���գ�x�����գ�x��=0����ʱ
��ʱ���գ�x�����գ�x��=0����ʱ ��0��
��0����
 ���գ�x���ڣ�
���գ�x���ڣ� ��x���ϵ����ݼ���
��x���ϵ����ݼ����൱x�ʣ�
 ��x��ʱ���գ�x�����գ�x��=0����ʱ
��x��ʱ���գ�x�����գ�x��=0����ʱ ��0��
��0����y=f��x���ڣ�0��
 ���ȣ�
���ȣ� ��+�ޣ��ϲ����ڡ���ԳƵ㡱��
��+�ޣ��ϲ����ڡ���ԳƵ㡱����
 ��
�� ��0��
��0����գ�x���ڣ�0��+�ޣ�������������
��x��xʱ���գ�x�����գ�x��=0��
��x��xʱ���գ�x�����գ�x��=0����
 ��0��
��0������ʱ��P��y=f��x���ġ���ԳƵ㡱
���ϣ�y=f��x�����ڡ���ԳƵ㡱��
 ��һ������ԳƵ㡱�ĺ����꣮
��һ������ԳƵ㡱�ĺ����꣮���������⿼�麯���ĵ������������̽�����㺯����һ������µIJ�������̽�������Ƿ���ڡ���ԳƵ㡱������ʱҪ�������⣬ע���������˼��͵ȼ�ת��˼��ĺ������ã����������⣮

��ϰ��ϵ�д�
�����Ŀ
 ��֪����f��x��=Asin����x+�գ���x��R��A��0���أ�0��|��|��
��֪����f��x��=Asin����x+�գ���x��R��A��0���أ�0��|��|��| �� |
| 2 |
A��f(x)=2sin(��x+
| ||
B��f(x)=2sin(2��x+
| ||
C��f(x)=2sin(��x+
| ||
D��f(x)=2sin(2��x+
|