题目内容
已知正项等比数列{an}满足a4=2a2+a3,a32=a6.
(Ⅰ)求{an}的通项公式;
(Ⅱ)求an•log2(an)的前n项和Tn.
(Ⅰ)求{an}的通项公式;
(Ⅱ)求an•log2(an)的前n项和Tn.
考点:数列的求和,等比数列的通项公式
专题:计算题,等差数列与等比数列
分析:(Ⅰ)利用方程组,即可求{an}的通项公式;
(Ⅱ)利用错位相减法,求an•log2(an)的前n项和Tn.
(Ⅱ)利用错位相减法,求an•log2(an)的前n项和Tn.
解答:
解:(Ⅰ)设等比数列{an}的首项为a1,公比为q(q>0),则
∵a4=2a2+a3,a32=a6,
∴a1q3=2a1q+a1q2,a12q4=a1q5,
∴a1=2,q=2;
(Ⅱ)an•log2(an)=n•2n,
∴Tn=1•2+2•22+…+n•2n,
∴2Tn=1•22+2•23+…+n•2n+1,
两式相减,整理可得Tn=(n-1)2n+1+2.
∵a4=2a2+a3,a32=a6,
∴a1q3=2a1q+a1q2,a12q4=a1q5,
∴a1=2,q=2;
(Ⅱ)an•log2(an)=n•2n,
∴Tn=1•2+2•22+…+n•2n,
∴2Tn=1•22+2•23+…+n•2n+1,
两式相减,整理可得Tn=(n-1)2n+1+2.
点评:本题考查等比数列的通项,考查数列求和,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知A,B两地的距离为10km,B,C两地的距离为40km,现测得∠ABC=120°,则A,C两地的距离为( )
A、10
| ||
B、10
| ||
C、10
| ||
D、10
|
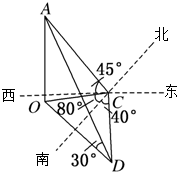 某人在C点测得某塔在南偏西80°的O处,塔顶A的仰角为45°,此人沿南偏东40°方向前进10米到D处,测得塔顶A的仰角为30°,求塔OA的高度?
某人在C点测得某塔在南偏西80°的O处,塔顶A的仰角为45°,此人沿南偏东40°方向前进10米到D处,测得塔顶A的仰角为30°,求塔OA的高度? 某高三7班30名男生1000米跑统测成绩的茎叶图(如果某学生1000米测试成绩是x分y秒,x为茎,y为叶)如图.
某高三7班30名男生1000米跑统测成绩的茎叶图(如果某学生1000米测试成绩是x分y秒,x为茎,y为叶)如图.