题目内容
在区间[-4,-
]上,函数f(x)=-x2+px+q与g(x)=x+
同时取得相同的最大值,那么函数f(x)在区间[-4,-
]上的最小值为______.
| 1 |
| 4 |
| 1 |
| x |
| 1 |
| 4 |
由题意得g′(x)=1-
,[-4,-
],
令g′(x)>0解得-4≤x<-1,令g′(x)<0解得-1<x≤-
,
所以g(x)在[-4,-1]上单调递增,在,[-1,-
]上单调递减,
所以g(x)在x=-1是取得最大值为-2.
所以f(x)=-x2+px+q在x=-1时取得最大值为-2.
解得p=-2,q=-3.
可得f(x)=-x2-2x-3,
所以当x=-4时函数f(x)有最小值为-11.
故答案为-11.
| 1 |
| x2 |
| 1 |
| 4 |
令g′(x)>0解得-4≤x<-1,令g′(x)<0解得-1<x≤-
| 1 |
| 4 |
所以g(x)在[-4,-1]上单调递增,在,[-1,-
| 1 |
| 4 |
所以g(x)在x=-1是取得最大值为-2.
所以f(x)=-x2+px+q在x=-1时取得最大值为-2.
解得p=-2,q=-3.
可得f(x)=-x2-2x-3,
所以当x=-4时函数f(x)有最小值为-11.
故答案为-11.

练习册系列答案
相关题目
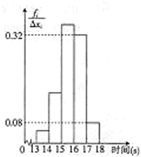 (2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
(2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.