题目内容
已知tanα=2求下列代数式的值:
(1)
(2)3sin2α-sinαcosα+1.
(1)
| 2sin2α-3cos2α | 4sin2α-9cos2α |
(2)3sin2α-sinαcosα+1.
分析:(1)原式分子分母除以cos2α,利用同角三角函数间基本关系化简,将tanα的值代入计算即可求出值;
(2)原式分母看做“1”,利用同角三角函数间基本关系化简,再弦化切后把tanα的值代入计算即可求出值.
(2)原式分母看做“1”,利用同角三角函数间基本关系化简,再弦化切后把tanα的值代入计算即可求出值.
解答:解:(1)∵tanα=2,
∴原式=
=
=
;
(2)∵tanα=2,
∴原式=
=
=
=
=3.
∴原式=
| 2tan2α-3 |
| 4tan2α-9 |
| 2×22-3 |
| 4×22-9 |
| 5 |
| 7 |
(2)∵tanα=2,
∴原式=
| 4sin2α-sinαcosα+cos2α |
| sin2α+cos2α |
| 4tan2α-tanα+1 |
| tan2α+1 |
| 4×22-2+1 |
| 22+1 |
| 15 |
| 5 |
点评:此题考查了同角三角函数间基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 ,设数列{bn}的前n项和为Rn.已知正实数λ满足:对任意正整数n,Rn≤λn恒成立,求λ的最小值.
,设数列{bn}的前n项和为Rn.已知正实数λ满足:对任意正整数n,Rn≤λn恒成立,求λ的最小值.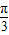 )(x∈R),且
)(x∈R),且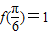 .
.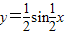 的图象;
的图象;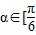 ,
,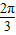 ,
,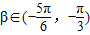 ,
,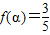 ,f(β)=-
,f(β)=- ,
,