题目内容
如四棱锥P―ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD//BC,CB⊥侧面PAB,△PAB是等边三角形,BC=1,DA=AB=2BC,F是线段AB的中点。
|
(1)求证:DF⊥PF;
(2)求PC与平面PDF所成的角。
解析:(1)证明:∵CB⊥侧面PAB,PF![]() 平面PAB,∴PF⊥BC,
平面PAB,∴PF⊥BC,
又∵△PAB是等边三角形,F是线段AB的中点,∴PF⊥AB,
![]() ∴PF⊥平面ABCD,
∴PF⊥平面ABCD,
而DF![]() 平面ABCD,∴DF⊥PF。……………………5分
平面ABCD,∴DF⊥PF。……………………5分
(2)方法一:
作CH⊥DF,垂足为H,连接PH,
由(1)知:PF⊥平面ABCD。
∴平面PDF⊥平面CDF,
∴CH⊥平面PDF,
∴PH是PC在平面PDF上的射影,
∴∠CPH是PC与平面PDF所成的角。
∵CB⊥侧面PAB,AD//BC,DA⊥侧面PAB,
∴△DAF,△BFC,△PBC都是直角三角形,
BC=1,则DA=AB=2,AF=FB=1,
在三角形DFC中,DF=![]()
![]() 可求得
可求得![]()
∴直角三角形PHC中,![]()
∴PC与平面PDF所成的角为![]() ……………………12分
……………………12分
方法二:
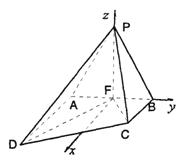
如图,以F为原点,建立空间直角坐标系。
|
BC=1,则DA=AB=2,AF=FB=1,PF=![]()
从而C(1,1,0)、D(2,-1,0)、P(0,0![]() )
)
![]()
设![]() 为平面PDF的法向量,由
为平面PDF的法向量,由
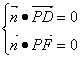 ,可求得
,可求得![]()
设PC与平面PDF所成的角为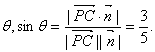
∴PC与平面PDF所成的角为![]() ……………………12分
……………………12分

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目

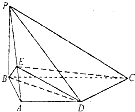 (2013•南京二模)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,PB⊥平面ABCD,CD⊥BD,PB=AB=AD=1,点E在线段PA上,且满足PE=2EA.
(2013•南京二模)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,PB⊥平面ABCD,CD⊥BD,PB=AB=AD=1,点E在线段PA上,且满足PE=2EA.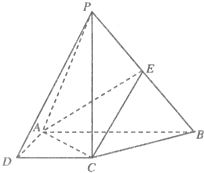 (2012•唐山二模)如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
(2012•唐山二模)如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.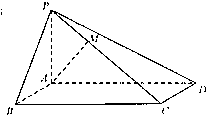 (2011•武昌区模拟)如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,BC=2AB=2PA.点M在侧棱PC上,且CM=2MP.
(2011•武昌区模拟)如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,BC=2AB=2PA.点M在侧棱PC上,且CM=2MP.