题目内容
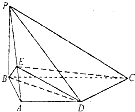 (2013•南京二模)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,PB⊥平面ABCD,CD⊥BD,PB=AB=AD=1,点E在线段PA上,且满足PE=2EA.
(2013•南京二模)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,PB⊥平面ABCD,CD⊥BD,PB=AB=AD=1,点E在线段PA上,且满足PE=2EA.(1)求三棱锥E-BAD的体积;
(2)求证:PC∥平面BDE.
分析:(1)先作垂线,求棱锥的高,再根据体积公式求棱锥的体积;
(2)根据在三角形中分相邻两边等比例的线段平行于底边,证线线平行,再由线线平行证明线面平行.
(2)根据在三角形中分相邻两边等比例的线段平行于底边,证线线平行,再由线线平行证明线面平行.
解答:解:(1)过E作EF⊥AB,垂足为F,
∵PB⊥平面ABCD,∴平面PAB⊥平面ABCD,
又平面PAB∩平面ABCD=AB,EF?平面PAB,
∴EF⊥平面ABCD,即EF为三棱锥E-BAD的高,
∵EF∥PB,PE=2EA,PB=1,∴EF=
,
∵CD⊥BD,梯形ABCD为直角梯形,∴∠A=90°,
∵AB=AD=1,∴VE-BAD=
×S△BAD×EF=
.
(2)证明:连接AC交BD与G,连接EG,
∵∠A=90°,AB=AD=1,∴BD=
,∠CBD=45°,
∵CD⊥BD,∴BC=2,
∵AD∥BC,BC=2,AD=1,∴
=
,
∵PE=2EA,∴EG∥PC,
又PC?平面BDE,EG?平面BDE,
∴PC∥平面BDE.
∵PB⊥平面ABCD,∴平面PAB⊥平面ABCD,
又平面PAB∩平面ABCD=AB,EF?平面PAB,
∴EF⊥平面ABCD,即EF为三棱锥E-BAD的高,

∵EF∥PB,PE=2EA,PB=1,∴EF=
| 1 |
| 3 |
∵CD⊥BD,梯形ABCD为直角梯形,∴∠A=90°,
∵AB=AD=1,∴VE-BAD=
| 1 |
| 3 |
| 1 |
| 18 |
(2)证明:连接AC交BD与G,连接EG,
∵∠A=90°,AB=AD=1,∴BD=
| 2 |
∵CD⊥BD,∴BC=2,
∵AD∥BC,BC=2,AD=1,∴
| AG |
| GC |
| 1 |
| 2 |
∵PE=2EA,∴EG∥PC,
又PC?平面BDE,EG?平面BDE,
∴PC∥平面BDE.
点评:本题考查线面平行的判定及棱锥的体积.

练习册系列答案
相关题目
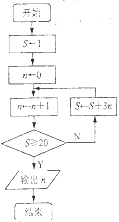 (2013•南京二模)如图是一个算法流程图,其输出的n的值是
(2013•南京二模)如图是一个算法流程图,其输出的n的值是