题目内容
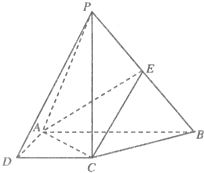 (2012•唐山二模)如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
(2012•唐山二模)如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.(I)求证:平面EAC⊥平面PBC;
( II)若PC=
| 2 |
分析:(Ⅰ)由题意可得AC⊥PC,由AC2+BC2=AB2,可求得AC⊥BC,从而有AC⊥平面PBC,利用面面垂直的判定定理即可证得平面EAC⊥平面PBC;
(Ⅱ)由PC=
,知△PBC为等腰直角三角形,又AC为三棱锥A-BCE高,设三棱锥C-ABE的高为h,由S△ABE•h=S△BCE•AC即可求得h.
(Ⅱ)由PC=
| 2 |
解答:解:(Ⅰ)∵PC⊥平面ABCD,AC?平面ABCD,
∴AC⊥PC,
∵AB=2,AD=CD=1,
∴AC=BC=
,
∴AC2+BC2=AB2,
∴AC⊥BC,
又BC∩PC=C,
∴AC⊥平面PBC,
∵AC?平面EAC,
∴平面EAC⊥平面PBC.…(5分)
(Ⅱ)由PC=
,知△PBC为等腰直角三角形,则S△BCE=
S△PBC=
,
由(Ⅰ)知,AC为三棱锥A-BCE高.…(7分)
∵Rt△PCA≌Rt△PCB≌Rt△ACB,PA=PB=AB=2,
∴S△ABE=
S△PAB=
,
设三棱锥C-ABE的高为h,
则
S△ABE•h=
S△BCE•AC,即
×
h=
×
×
,
∴h=
,
∴三棱锥C-ABE的高等于
.…(12分)
∴AC⊥PC,
∵AB=2,AD=CD=1,
∴AC=BC=
| 2 |
∴AC2+BC2=AB2,
∴AC⊥BC,
又BC∩PC=C,
∴AC⊥平面PBC,
∵AC?平面EAC,
∴平面EAC⊥平面PBC.…(5分)
(Ⅱ)由PC=
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由(Ⅰ)知,AC为三棱锥A-BCE高.…(7分)
∵Rt△PCA≌Rt△PCB≌Rt△ACB,PA=PB=AB=2,
∴S△ABE=
| 1 |
| 2 |
| ||
| 2 |
设三棱锥C-ABE的高为h,
则
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
∴h=
| ||
| 3 |
∴三棱锥C-ABE的高等于
| ||
| 3 |
点评:本题考查平面与平面垂直的判定,考查点、线、面间的距离计算,突出几何体体积轮换公式的考查与应用,属于中档题.

练习册系列答案
相关题目
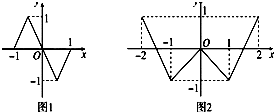 (2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )
(2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )