题目内容
已知等比数列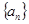 的首项
的首项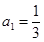 ,公比
,公比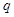 满足
满足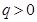 且
且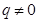 ,又已知
,又已知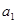 ,
,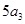 ,
,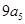 ,成等差数列;
,成等差数列;
求数列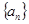 的通项;
的通项;
令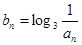 ,求
,求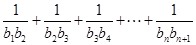 的值;
的值;
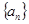 的首项
的首项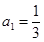 ,公比
,公比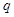 满足
满足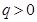 且
且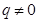 ,又已知
,又已知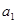 ,
,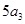 ,
,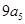 ,成等差数列;
,成等差数列;求数列
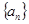 的通项;
的通项;令
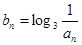 ,求
,求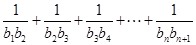 的值;
的值;(1) ;(2)
;(2) ;
;
 ;(2)
;(2) ;
;试题分析:(1)利用
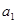 ,
,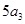 ,
,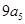 成等差数列得到一个式子,然后将式子中的
成等差数列得到一个式子,然后将式子中的 ,
, 换成
换成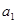 ,
,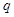 得出
得出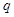 ,通项公式得解;(2)把(1)问中求得的
,通项公式得解;(2)把(1)问中求得的 代入式子
代入式子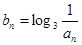 得
得 的通项公式,将通项代入
的通项公式,将通项代入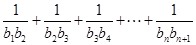 得到
得到 ,通过观察可发现求这个式子的和可以通过列项求和得到;
,通过观察可发现求这个式子的和可以通过列项求和得到;试题解析:(1)解:在等比数列
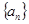 中,
中, ,
, 成等差数列,
成等差数列,
即:

 解得:
解得:
又




(2)解:
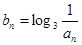


=

=
 =
=

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
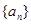 的前
的前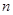 项和
项和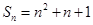 ,
, ,数列
,数列 的前n项和为
的前n项和为 ,点
,点 在曲线
在曲线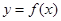 上
上 ,且
,且 .
.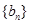 的前n项和为
的前n项和为 ,且满足
,且满足 ,问:当
,问:当 为何值时,数列
为何值时,数列 中,
中, ,对
,对 总有
总有 成立,
成立, 的值;
的值; ,并用数学归纳法证明
,并用数学归纳法证明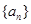 满足
满足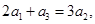 且
且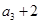 是
是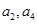 的等差中项
的等差中项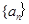 的通项公式;(2)若
的通项公式;(2)若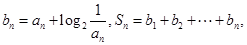 求使
求使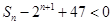 成立的正整数
成立的正整数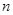 的最小值.
的最小值. 时,数列{an}为递减数列;②当
时,数列{an}为递减数列;②当 为正整数时,数列{an}必有两项相等的最大项
为正整数时,数列{an}必有两项相等的最大项 的前n项和是Sn,若
的前n项和是Sn,若 都是等差数列,且公差相等,则数列
都是等差数列,且公差相等,则数列



 前项和为
前项和为 ,且点
,且点 在
在 图像上,求
图像上,求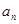
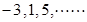 的第15项为( )
的第15项为( )