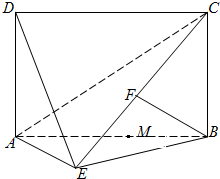
题目内容
如图,在底面为平行四边形的四棱柱 中,
中,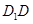
 底面
底面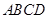 ,
, ,
,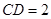 ,
,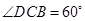 .
.
(1)求证:平面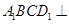 平面
平面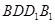 ;
;
(2)若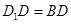 ,求四棱锥
,求四棱锥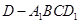 的体积.
的体积.
(1)详见解析;(2)四棱锥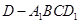 的体积为
的体积为 .
.
解析试题分析:(1)要证平面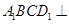 平面
平面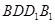 ,只需要证明
,只需要证明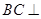 平面
平面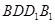 ,先利用余弦定理求出
,先利用余弦定理求出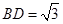 ,再由勾股定理得到
,再由勾股定理得到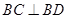 ,结合
,结合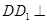 平面
平面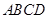 可得到
可得到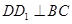 ,由这两个条件可以证明
,由这两个条件可以证明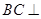 平面
平面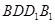 ,最终利用平面与平面垂直的判定定理可以证明平面
,最终利用平面与平面垂直的判定定理可以证明平面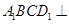 平面
平面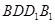 ;
;
(2)先由已知条件结合(1)中的数据得到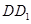 的长度,先由(1)中的结论
的长度,先由(1)中的结论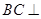 平面
平面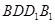 得出四边形
得出四边形 为矩形,从而可以计算出矩形
为矩形,从而可以计算出矩形 的面积,然后取
的面积,然后取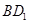 的中点,连接
的中点,连接 ,利用(1)中的结论结合平面与平面垂直的性质定理得到
,利用(1)中的结论结合平面与平面垂直的性质定理得到 平面
平面 ,并计算出
,并计算出 的长度,最终利用锥体体积公式计算出四棱锥
的长度,最终利用锥体体积公式计算出四棱锥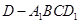 的体积;解法二是将四棱锥
的体积;解法二是将四棱锥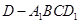 分解为两个三棱锥
分解为两个三棱锥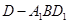 和三棱锥
和三棱锥 ,利用两个三棱锥等底同高得到两个三棱锥的体积相等,从而得到
,利用两个三棱锥等底同高得到两个三棱锥的体积相等,从而得到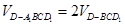 ,在计算三棱锥
,在计算三棱锥 的体积时,利用等体积法计算三棱锥
的体积时,利用等体积法计算三棱锥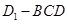 的体积,此时
的体积,此时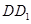 为高,
为高, 为底,从而计算出三棱锥
为底,从而计算出三棱锥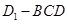 的体积,最终得到四棱锥
的体积,最终得到四棱锥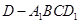 的体积.
的体积.
试题解析:(1)证明: 在 中,由余弦定理得:
中,由余弦定理得: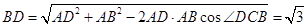 ,
,
所以 ,所以
,所以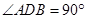 ,即
,即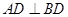 , 3分
, 3分
又四边形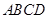 为平行四边形,所以
为平行四边形,所以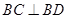 ,
,
又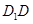
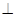 底面
底面 ,
,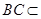 底面
底面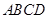 ,所以
,所以 , 4分
, 4分
又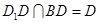 ,所以
,所以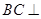 平面
平面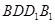 , 5分
, 5分
又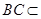 平面
平面 ,所以平面
,所以平面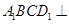 平面
平面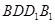 . 6分
. 6分
(2)法一:连结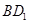 ,∵
,∵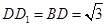 ,∴
,∴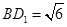
∵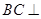 平面
平面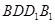 ,所以
,所以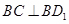 , 8分
, 8分
所以四边形 的面积
的面积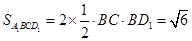 , 10分
, 10分
取 的中点
的中点 ,连结
,连结 ,则
,则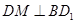 ,且
,且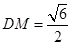 ,
,
又平面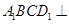 平面
平面 ,
,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,四边形
中,四边形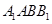 为菱形,
为菱形,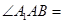
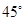 ,四边形
,四边形 为矩形,若
为矩形,若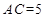 ,
,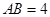 ,
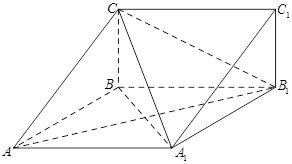
,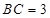 .
.
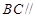 平面
平面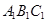 ;
;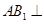 面
面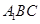 ;
;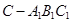 的体积.
的体积.
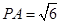 ,
,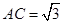 ,PB与底面ABC成60°角,
,PB与底面ABC成60°角,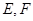 分别是
分别是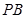 与
与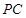 的中点,
的中点,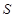 是线段
是线段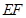 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体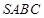 的体积。
的体积。 为矩形,
为矩形, 平面
平面 ,
, 为
为 上的点,且
上的点,且 平面
平面 .
. 
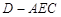 的体积;
的体积; 在线段
在线段 上,且满足
上,且满足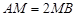 ,试在线段
,试在线段 ,使得
,使得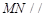 平面
平面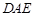 .
.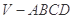 中,底面
中,底面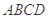 是正方形,侧面
是正方形,侧面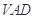 是正三角形,平面
是正三角形,平面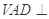 底面
底面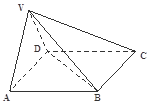
 为线段VC的中点,求证:
为线段VC的中点,求证: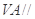 平面
平面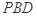 ;
;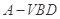 的体积
的体积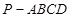 的底面是正方形,
的底面是正方形,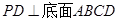 ,点
,点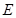 在棱
在棱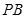 上.
上.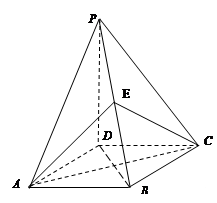
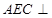 平面
平面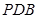 ;
;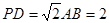 ,且
,且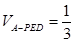 时,确定点
时,确定点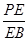 的值.
的值.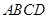 是正方形,
是正方形,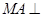 平面
平面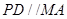 ,
,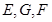 分别为
分别为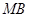 ,
,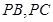 的中点,且
的中点,且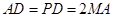 .
.
 平面
平面 ;
; 与四棱锥
与四棱锥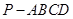 的体积之比.
的体积之比.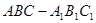 ,底面三角形
,底面三角形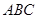 为正三角形,侧棱
为正三角形,侧棱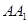
 底面
底面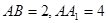 ,
, 为
为 为
为 中点.
中点.
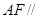 平面
平面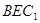 ;
;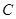 到平面
到平面 的正方体
的正方体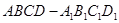 中分离出来的:
中分离出来的: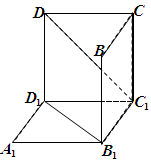
 是否在平面
是否在平面 内;(回答是与否)
内;(回答是与否) 与
与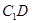 所成的角;
所成的角;