Question

解不等式2＜|2x－5|≤7.?

Answer 1

解法一：原不等式等价于

∴

即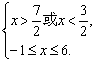

∴原不等式的解集为{x|－1≤x＜或＜x≤6}.?

解法二：原不等式的解集是下面两个不等式组解集的并集.

（Ⅰ）

（Ⅱ）

不等式组（Ⅰ）的解集为{x|＜x≤6}，?

不等式组（Ⅱ）的解集是{x|－1≤x＜}.?

∴原不等式的解集是{x|－1≤x＜或＜x≤6}.?

解法三：原不等式的解集是下面两个不等式解集的并集.?

（Ⅰ）2＜2x－5≤7,?

（Ⅱ）2＜5－2x≤7.?

不等式（Ⅰ）的解集为{x|＜x≤6},?

不等式（Ⅱ）的解集是{x|－1≤x＜}.?

∴原不等式的解集是{x|－1≤x＜或＜x≤6}.?

点评：含绝对值的双向不等式的解法，关键是去绝对值号.其方法一是转化为单向不等式组如解法一，再就是利用绝对值的定义如解法二、解法三.