题目内容
如图,四棱锥 的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(Ⅰ) 求证:平面AEC⊥平面PDB;
(Ⅱ) 当PD= AB,且E为PB的中点时,求AE与平面PDB所成的角的大小.
AB,且E为PB的中点时,求AE与平面PDB所成的角的大小.

解:(1)证明 ∵四边形ABCD是正方形,
∴AC⊥BD.∵PD⊥底面ABCD,
∴PD⊥AC.又PD∩BD=D,
∴AC⊥平面PDB.又AC⊂平面AEC,
∴平面AEC⊥平面PDB.-------------------6分
(2)解 设AC∩BD=O,连接OE.
由(1)知,AC⊥平面PDB于点O,
∴∠AEO为AE与平面PDB所成的角.
∵点O、E分别为DB、PB的中点,∴OE∥PD,且OE= PD.
PD.
又∵PD⊥底面ABCD,∴OE⊥底面ABCD,∴OE⊥AO.
在Rt△AOE中,OE= PD=
PD= AB=AO,∴∠AEO=45°.
AB=AO,∴∠AEO=45°.
即AE与平面PDB所成的角为45°-------------------12分.

练习册系列答案
相关题目
某公司的广告费支出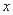 与销售额
与销售额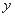 (单位:万元)之间有下列对应数据:由资料显示
(单位:万元)之间有下列对应数据:由资料显示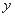 对
对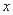 呈线性相关关系。
呈线性相关关系。
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
根据上表提供的数据得到回归方程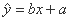 中的
中的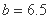 ,预测销售额为115万元时约
,预测销售额为115万元时约
需 万元广告费.
 中,
中, 、
、 、
、 分别为角
分别为角 、
、 、
、 所对的边,若
所对的边,若 ,则此三角形一定是 三角形.
,则此三角形一定是 三角形. ,
, 的倾斜角为( )
的倾斜角为( ) B.
B. C.
C. D.
D.
 是二面角
是二面角 的棱
的棱 上一点,分别在
上一点,分别在 上引射线
上引射线 、
、 ,截
,截 ,如果∠
,如果∠ ∠
∠
 ,∠
,∠ ,则二面角
,则二面角
 ( )
( ) 的图像,只需将
的图像,只需将 的图像( )
的图像( ) 个单位 B 向右平移
个单位 B 向右平移 个单位 D 向右平移
个单位 D 向右平移 ,则不等式
,则不等式 的解集是
的解集是 B.
B. C.[1,ln3] D.
C.[1,ln3] D.
 的前
的前 项和为
项和为 .若
.若 且
且 则
则 .
.