题目内容
1.直线l过点P(1,4)分别交x轴的正方向和y轴正方向于A、B两点.①当|OA|+|OB|最小时,求l的方程.
②当|PA|•|PB|最小时,求l的方程.
分析 ①由已知直线l的斜率k<0,设直线l的方程为y-4=k(x-1),则A($-\frac{4}{k}+1$,0),B(0,-k+4),由此利用均值定理能求出|OA|+|OB|最小时直线l的方程.
②由|PA|•|PB|=$\sqrt{(-\frac{4}{k}+1-1)^{2}+{4}^{2}}$•$\sqrt{{1}^{2}+(-k+4-4)^{2}}$,利用均值定理能求出当|PA|•|PB|最小时,直线l的方程.
解答 解:①∵直线l过点P(1,4)分别交x轴的正方向和y轴正方向于A、B两点,
∴直线l的斜率k<0,设直线l的方程为y-4=k(x-1),
则A($-\frac{4}{k}+1$,0),B(0,-k+4),
∴|OA|+|OB|=-$\frac{4}{k}+1+(-k+4)$
=(-$\frac{4}{k}$-k)+5≥2$\sqrt{(-\frac{4}{k})•(-k)}$+5=9,
当且仅当k=-2时取等号,∴l的方程为y-4=-2(x-1),
即2x+y-6=0.
②由①知|PA|•|PB|=$\sqrt{(-\frac{4}{k}+1-1)^{2}+{4}^{2}}$•$\sqrt{{1}^{2}+(-k+4-4)^{2}}$
=$\sqrt{\frac{16({k}^{2}+1)^{2}}{{k}^{2}}}$=-$\frac{4}{k}({k}^{2}+1)$=4(-$\frac{1}{k}-k$)≥4$•2\sqrt{(-\frac{1}{k})•(-k)}$=8,
当且仅当k=-1时取等号,
∴l的方程为y-4=-(x-1),即x+y-5=0.
点评 本题考查直线方程的求法,是中档题,解题时要认真审题,注意均值定理的合理运用.

练习册系列答案
相关题目
12.已知|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=5,$\overrightarrow{a}$与$\overrightarrow{b}$不共线,若向量k$\overrightarrow{a}$+$\overrightarrow{b}$与k$\overrightarrow{a}$-$\overrightarrow{b}$互相垂直,则实数k的值为( )
| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | ±$\frac{3}{5}$ | D. | ±$\frac{5}{3}$ |
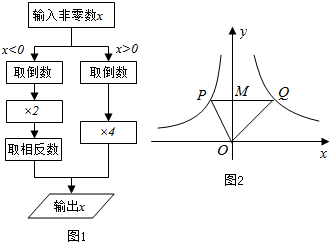
12.根据图1所示的程序,得到了y与x的函数图象,如图2.若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.则以下结论:
①x<0 时,y=$\frac{2}{x}$
②△OPQ的面积为定值.
③x>0时,y随x的增大而增大.
④MQ=2PM.
⑤∠POQ可以等于90°.其中正确结论是( )
①x<0 时,y=$\frac{2}{x}$
②△OPQ的面积为定值.
③x>0时,y随x的增大而增大.
④MQ=2PM.
⑤∠POQ可以等于90°.其中正确结论是( )

| A. | ①②④ | B. | ②④⑤ | C. | ③④⑤ | D. | ②③⑤ |
6.函数y=$\frac{lg(x+1)}{x-2}$的定义域是( )
| A. | (-1,+∞) | B. | [-1,+∞) | C. | (-1,2)∪(2,+∞) | D. | [-1,2)∩(2,+∞) |