题目内容
在△ABC中,满足tanA•tanB>1,则这个三角形是( )
分析:由条件可得A、B都是锐角,tanA>0,tanB>0,再由 tan(A+B)=
<0,可得A+B为钝角,C为锐角,与偶此得出结论.
| tanA+tanB |
| 1-tanA•tanB |
解答:解:∵在△ABC中,满足tanA•tanB>1,∴A、B都是锐角,tanA>0,tanB>0.
再由 tan(A+B)=
<0,可得A+B为钝角,故由三角形内角和公式可得C为锐角.
综上可得这个三角形是锐角三角形.
故选C.
再由 tan(A+B)=
| tanA+tanB |
| 1-tanA•tanB |
综上可得这个三角形是锐角三角形.
故选C.
点评:本题主要考查两角和的正切公式、三角形内角和公式的应用,判断三角形的形状,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,在△ABC中,AD⊥BC,
如图,在△ABC中,AD⊥BC,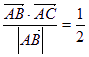 ,
,  , 又点E在BC边上, 且满足
, 又点E在BC边上, 且满足 ),为奇函数,则a=1;
),为奇函数,则a=1; ,其中θ∈(π,
,其中θ∈(π, ),则
),则
 =a,
=a, =b,若a•b<0,则△ABC是钝角三角形
=b,若a•b<0,则△ABC是钝角三角形 ,λ∈(0,+∞),则直线AP一定通过△ABC的内心.
,λ∈(0,+∞),则直线AP一定通过△ABC的内心.