题目内容
一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船是每小时航行
10海里
10海里
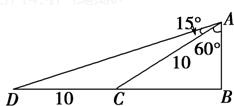
.分析:如图,依题意有∠BAC=60°,∠BAD=75°,所以∠CAD=∠CDA=15°,从而CD=CA=10,在直角三角形ABC中,得AB=5,由此能求出这艘船的速度.
解答: 解:如图,依题意有∠BAC=60°,∠BAD=75°,
解:如图,依题意有∠BAC=60°,∠BAD=75°,
所以∠CAD=∠CDA=15°,
从而CD=CA=10,
在直角三角形ABC中,得AB=5,
于是这艘船的速度是
=10(海里/小时).
故答案为:10海里.
 解:如图,依题意有∠BAC=60°,∠BAD=75°,
解:如图,依题意有∠BAC=60°,∠BAD=75°,所以∠CAD=∠CDA=15°,
从而CD=CA=10,
在直角三角形ABC中,得AB=5,
于是这艘船的速度是
| 5 |
| 0.5 |
故答案为:10海里.
点评:本题考查三角形知识的实际运用,解题时要注意数形结合思想的灵活运用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时( )
一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时( )| A、5海里 | ||
B、5
| ||
| C、10海里 | ||
D、10
|