题目内容
一船向正北航行,看见正西方向有相距20海里的两个灯塔恰好与它在一条直线上继续航行l小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西30°,则这只船的速度是每小时
10
| 3 |
10
海里.| 3 |
分析:设该船的位置是从B到A,两个灯塔位置分别为C、D,如图所示.根据题意,得到△ACD中∠CAD=∠CDA=30°,从而CD=CA=20,在Rt△ABC中利用三角函数的定义算出AB=10
海里,即可得到该船的时速.
| 3 |
解答:解:如图,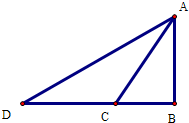 设该船的位置是从B到A,两个灯塔位置分别为C、D
设该船的位置是从B到A,两个灯塔位置分别为C、D
依题意有AB⊥BD,∠BAD=60°,∠BAC=30°,
所以∠CAD=∠CDA=30°,
从而CD=CA=20,
在Rt△ABC中,得AB=ACcos30°=10
,
∴这艘船的速度是10
(海里/小时).
故答案为:10
 设该船的位置是从B到A,两个灯塔位置分别为C、D
设该船的位置是从B到A,两个灯塔位置分别为C、D依题意有AB⊥BD,∠BAD=60°,∠BAC=30°,
所以∠CAD=∠CDA=30°,
从而CD=CA=20,
在Rt△ABC中,得AB=ACcos30°=10
| 3 |
∴这艘船的速度是10
| 3 |
故答案为:10
| 3 |
点评:本题给出实际应用问题,求轮船的航行时速.着重考查了解直角三角形和方位角等概念,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
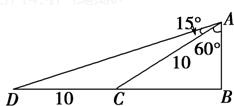 一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时( )
一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时( )| A、5海里 | ||
B、5
| ||
| C、10海里 | ||
D、10
|