题目内容
已知函数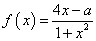 在区间
在区间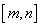 上为增函数,且
上为增函数,且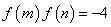 。
。
(1)当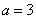 时,求
时,求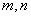 的值;(2)当
的值;(2)当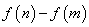 最小时,①求
最小时,①求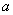 的值; ②若
的值; ②若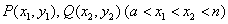 是
是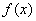 图象上的两点,且存在实数
图象上的两点,且存在实数 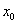 使得
使得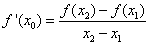 ,证明:
,证明: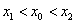 。
。
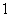 解:
解: 。(1)当
。(1)当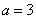 时,由
时,由 ,得
,得 或
或 ,
,
所以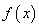 在
在 上为增函数,在
上为增函数,在 ,
, 上为减函数,由题意知
上为减函数,由题意知 ,且
,且 。因为
。因为 ,所以
,所以 ,
,
可知 。 (2)① 因为
。 (2)① 因为 ,
,
当且仅当 时等号成立。由
时等号成立。由 ,有
,有 ,得
,得 ;由
;由 ,有
,有 ,得
,得 ;故
;故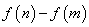 取得最小值时,
取得最小值时, ,
, 。②此时,
。②此时, ,
, , 由
, 由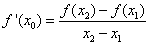 知,
知, ,欲证
,欲证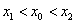 ,先比较
,先比较 与
与 的大小。
的大小。


 因为
因为 ,所以
,所以 ,有
,有 ,
,
于是 ,即
,即 ,另一方面,
,另一方面, ,因为
,因为 ,所以
,所以 ,从而
,从而 ,即
,即 。…14分同理可证
。…14分同理可证 ,因此
,因此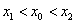 。
。

练习册系列答案
相关题目
 的解集为
的解集为 ,则函数
,则函数 的图象为( )
的图象为( )
 上的函数
上的函数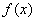 满足
满足 且
且 时,
时, 则
则 ( )A.
( )A. B.
B. C.
C. D.
D.
 .(Ⅰ)证明:当
.(Ⅰ)证明:当 时,
时, ;(Ⅱ)设当
;(Ⅱ)设当 时,
时, ,求a的取值范围.
,求a的取值范围.  满足:
满足: ,当
,当 时,
时, .下列四个不等关系:
.下列四个不等关系: ;
; ;
; ;
; .其中正确的个数是 .
.其中正确的个数是 .  的最大值为
的最大值为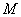 ,最小值为
,最小值为 ,那么
,那么 .
. 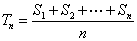 ,称Tn为数列a1,a2,…,an的“理想数”.已知a1,a2,…,a500的“理想数”为1002,那么数列3,a1,a2,….a500的“理想数”为 ( ) A.1001 B.1003 C.1004 D.1005
,称Tn为数列a1,a2,…,an的“理想数”.已知a1,a2,…,a500的“理想数”为1002,那么数列3,a1,a2,….a500的“理想数”为 ( ) A.1001 B.1003 C.1004 D.1005 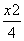 -y2=1,x、y∈R},Q={(x,y)|x=an,y=
-y2=1,x、y∈R},Q={(x,y)|x=an,y=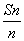 ,n∈N*},给出下列命题:
,n∈N*},给出下列命题: