题目内容
5．抛物线y2=4x的焦点坐标是（ ）| A． | （1，0） | B． | （0，1） | C． | （2，0） | D． | （0，2） |
分析 由抛物线y2=2px的焦点坐标为（$\frac{p}{2}$，0），即有p=2，即可得到焦点坐标．
解答 解：由抛物线y2=2px的焦点坐标为（$\frac{p}{2}$，0），
即有抛物线y2=4x的2p=4，即p=2，
则焦点坐标为（1，0），
故选：A．
点评 本题考查抛物线的方程和性质，主要考查抛物线的焦点，属于基础题．
练习册系列答案
相关题目
指数函数
单调递增；命题
，
.若命题“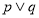
”为真命题，命题“
”为假命题，求实数
的取值范围.
满足
，则
的最小值为 . 
为极点，
轴的非负半轴为极轴建立极坐标系．已知点
的极坐标为
，曲线 
的参数方程为
（
为参数）．
过
且与曲线
相切，求直线
的极坐标方程；
与点
关于
轴对称，求曲线
上的点到点
的距离的取值范围．
的顶点都在抛物线
上，且
，则点
到抛物线的焦点的距离是_____________．
17．已知点P为曲线xy-$\frac{5}{2}$x-2y+3=0上任意一点，O为坐标原点，则|OP|的最小值为（ ）
| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{\sqrt{6}}{2}$ | C． | $\sqrt{2}$ | D． | $\frac{2\sqrt{3}}{3}$ |
14．若x，y满足$\left\{\begin{array}{l}kx+y≤4\\ 2y-x≤4\\ x≥0\\ y≥0\end{array}\right.$，且z=5y-x的最小值为-8，则k的值为（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -2 | D． | 2 |
某中学为了检验1000名在校高三学生对函数模块掌握的情况，进行了一次测试，并把成绩进行统计，得到的样本频率分布直方图如图所示，则考试成绩的中位数大约（保留两位有效数字）为（ ）