题目内容
函数的图象与方程的曲线有着密切的联系,如把抛物线y2=x的图象绕原点沿逆时针方向旋转90°就得到函数y=x2的图象.若把双曲线 绕原点按逆时针方向旋转一定角度θ后,能得到某一个函数的图象,则旋转角θ可以是( )
绕原点按逆时针方向旋转一定角度θ后,能得到某一个函数的图象,则旋转角θ可以是( )A.30°
B.45°
C.60°
D.90°
【答案】分析:确定双曲线的渐近线方程,求出倾斜角,即可得到结论.
解答: 解:双曲线
解:双曲线 的渐近线方程为
的渐近线方程为 ,其倾斜角为30°或150°
,其倾斜角为30°或150°
在双曲线 上取点(m,n),关于
上取点(m,n),关于 对称点的坐标为(x,y),则
对称点的坐标为(x,y),则 ,∴
,∴
∵ ,∴
,∴ 此时,是一个函数的图象
此时,是一个函数的图象
故把双曲线 绕原点按逆时针方向旋转60°时,双曲线方程为
绕原点按逆时针方向旋转60°时,双曲线方程为 ,双曲线的渐近线方程为x=0,与
,双曲线的渐近线方程为x=0,与 ,图象如图所示
,图象如图所示
故选C.
点评:本题考查双曲线的标准方程与性质,考查图象变换,属于中档题.
解答:
 解:双曲线
解:双曲线 的渐近线方程为
的渐近线方程为 ,其倾斜角为30°或150°
,其倾斜角为30°或150°在双曲线
 上取点(m,n),关于
上取点(m,n),关于 对称点的坐标为(x,y),则
对称点的坐标为(x,y),则 ,∴
,∴
∵
 ,∴
,∴ 此时,是一个函数的图象
此时,是一个函数的图象故把双曲线
 绕原点按逆时针方向旋转60°时,双曲线方程为
绕原点按逆时针方向旋转60°时,双曲线方程为 ,双曲线的渐近线方程为x=0,与
,双曲线的渐近线方程为x=0,与 ,图象如图所示
,图象如图所示故选C.
点评:本题考查双曲线的标准方程与性质,考查图象变换,属于中档题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
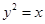 的图象绕原点沿逆时针方向旋转
的图象绕原点沿逆时针方向旋转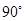 就得到函数
就得到函数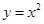 的图象.若把双曲线
的图象.若把双曲线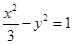 绕原点按逆时针方向旋转一定角度
绕原点按逆时针方向旋转一定角度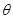 后,能得到某一个函数的图象,则旋转角
后,能得到某一个函数的图象,则旋转角 B.
B.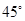 C.
C.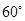 D.
D. 的曲线恰好有两个不同的公共点,则实数
的曲线恰好有两个不同的公共点,则实数 的取值范围是
的取值范围是  C、
C、 D、
D、
 的图象绕原点沿逆时针方向旋转
的图象绕原点沿逆时针方向旋转 就得到函数
就得到函数 的图象.若把双曲线
的图象.若把双曲线 绕原点按逆时针方向旋转一定角度
绕原点按逆时针方向旋转一定角度 后,能得到某一个函数的图象,则旋转角
后,能得到某一个函数的图象,则旋转角 B.
B. C.
C. D.
D.