题目内容
(本题满分14分)
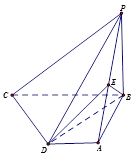
如图,已知平面QBC与直线PA均垂直于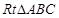 所在平面,且PA=AB=AC.
所在平面,且PA=AB=AC.
(Ⅰ)求证:PA∥平面QBC;
(Ⅱ)若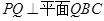 ,求二面角Q-PB-A的余弦值。
,求二面角Q-PB-A的余弦值。
(1)通过已知中的平面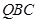 ⊥平面
⊥平面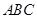 ,那么结合
,那么结合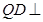 平面
平面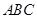 ,和
,和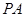 ⊥平面
⊥平面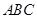 ,从而得到线线平行
,从而得到线线平行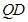 ∥
∥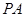 ,利用线面平行的性质来证明。
,利用线面平行的性质来证明。
(2) 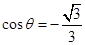
解析试题分析:解:(I)证明:过点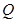 作
作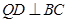 于点
于点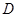 ,
,
∵平面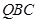 ⊥平面
⊥平面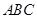 ∴
∴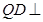 平面
平面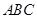
又∵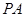 ⊥平面
⊥平面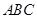
∴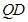 ∥
∥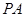 又∵
又∵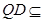 平面
平面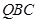
∴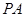 ∥平面
∥平面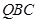 ……6分
……6分
(Ⅱ)∵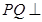 平面
平面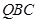
∴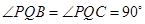 又∵
又∵
∴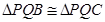 ∴
∴
∴点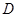 是
是 的中点,连结
的中点,连结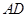 ,则
,则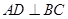
∴ 平面
平面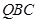 ∴
∴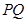 ∥
∥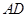 ,
,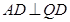
∴四边形 是矩形 ……8分
是矩形 ……8分
设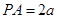
∴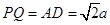 ,
,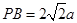 ∴
∴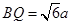
过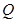 作
作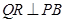 于点
于点 ,
,
∴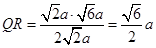 ,
,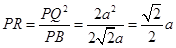
取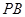 中点
中点 ,连结
,连结 ,取
,取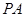 的中点
的中点 ,连结
,连结
∵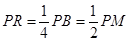 ,
, ∴
∴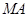 ∥
∥
∵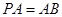 ∴
∴ ∴
∴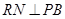
∴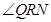 为二面角
为二面角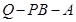 的平面角……12分
的平面角……12分
连结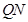 ,则
,则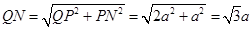 又∵
又∵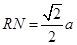
∴
即二面角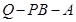 的余弦值为
的余弦值为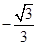 ……14分
……14分
方法二:
(I)同方法一 ……………………………………6分
(Ⅱ)∵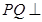 平面
平面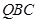
∴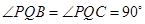 ,又∵
,又∵
∴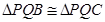 ∴
∴
∴点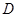 是
是 的中点,连结
的中点,连结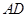 ,则
,则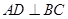
∴ 平面
平面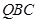 ∴
∴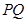 ∥
∥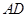 ,
,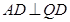
∴四边形
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
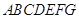 中,平面
中,平面 ∥平面
∥平面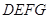 ,
,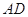 ⊥平面
⊥平面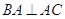 ,
,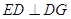 ,
,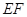 ∥
∥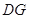 .
.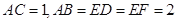 ,
, 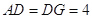 .
.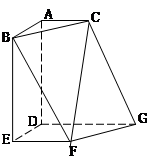
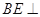 平面
平面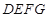 ;
;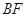 ∥平面
∥平面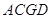 ;
;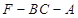 的余弦值.
的余弦值. 中,E为AC中点
中,E为AC中点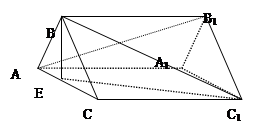

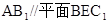 ,
, 是边长为4的正三角形,平面SAC⊥平面ABC,SA =" SC" =
是边长为4的正三角形,平面SAC⊥平面ABC,SA =" SC" = ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
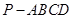 中,已知 PA⊥平面ABCD,
中,已知 PA⊥平面ABCD, 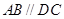 ,
, 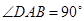 ,
,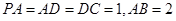 ,
, 为
为 的中点.
的中点.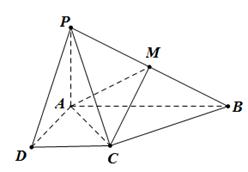
 的平面角的正切值.
的平面角的正切值.
 .
.
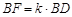 ,当二面角
,当二面角 为直二面角时,求k的值.
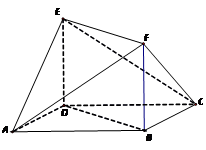
为直二面角时,求k的值.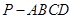 中,
中,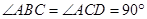 ,
,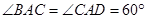 ,
, 平面
平面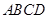 ,
,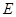 为
为 的中点,
的中点, .
.
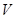 ;
;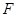 为
为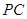 的中点,求证:平面
的中点,求证:平面 平面
平面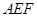 ;
;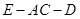 的大小。.
的大小。. 底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.