题目内容
四面体P-ABC中,若PA⊥平面ABC,当添加一个条件________后,该四面体各个面中直角三角形最多.
∠ABC=90°或∠ACB=90°
分析:由已知中四面体P-ABC中,若PA⊥平面ABC,则四面体中至少存在面PAB与面PAC一定是直角三角形,分别讨论∠BAC=90°,∠ABC=90°,∠ACB=90°三种情况下直角三角形的个数,即可得到答案.
解答:∵四面体P-ABC的四个面为四个三角形
又∵PA⊥平面ABC
故面PAB与面PAC一定是直角三角形
若∠BAC=90°时,
则面ABC为直角三角形,但面PBC不是直角三角形,此时直角三角形有3个;
若∠ABC=90°,则面ABC为直角三角形,且面PBC也是直角三角形,此时直角三角形有4个;
或∠ACB=90°,则面ABC为直角三角形,且面PBC也是直角三角形,此时直角三角形有4个;
故答案为:∠ABC=90°或∠ACB=90°
点评:本题考查的知识点是直线与平面垂直的性质,直线与平面垂直的判定,其中熟练掌握空间中线线垂直与线面垂直的相互转化,是解答本题的关键.
分析:由已知中四面体P-ABC中,若PA⊥平面ABC,则四面体中至少存在面PAB与面PAC一定是直角三角形,分别讨论∠BAC=90°,∠ABC=90°,∠ACB=90°三种情况下直角三角形的个数,即可得到答案.
解答:∵四面体P-ABC的四个面为四个三角形
又∵PA⊥平面ABC
故面PAB与面PAC一定是直角三角形
若∠BAC=90°时,
则面ABC为直角三角形,但面PBC不是直角三角形,此时直角三角形有3个;
若∠ABC=90°,则面ABC为直角三角形,且面PBC也是直角三角形,此时直角三角形有4个;
或∠ACB=90°,则面ABC为直角三角形,且面PBC也是直角三角形,此时直角三角形有4个;
故答案为:∠ABC=90°或∠ACB=90°
点评:本题考查的知识点是直线与平面垂直的性质,直线与平面垂直的判定,其中熟练掌握空间中线线垂直与线面垂直的相互转化,是解答本题的关键.

练习册系列答案
相关题目
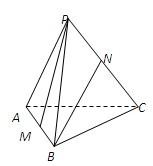 如图,已知正四面体P-ABC中,棱AB、PC的中点分别是M、N.
如图,已知正四面体P-ABC中,棱AB、PC的中点分别是M、N.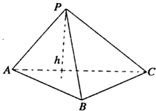 在Rt△ABC中,CA⊥CB,斜边AB上的高为h1,则
在Rt△ABC中,CA⊥CB,斜边AB上的高为h1,则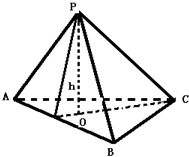 在Rt△ABC中,CA⊥CB,斜边AB上的高为
在Rt△ABC中,CA⊥CB,斜边AB上的高为