题目内容
7.在△ABC中,内角A、B、C所对的边分别为a,b,c,$B={60°},b=\sqrt{3}$.(1)求a+c的最大值;
(2)若△ABC为锐角三角形,求△ABC面积的取值范围.
分析 (1)由余弦定理,可得:(a+c)2=3ac+3,利用基本不等式可求3≥ac,从而可求a+c的最大值.
(2)由正弦定理可求$\frac{a}{sinA}=\frac{c}{sinC}=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}=2$,利用三角形面积公式,三角函数恒等变换的应用可求S△ABC=$\frac{\sqrt{3}}{2}$sin(2A-30°)+$\frac{\sqrt{3}}{4}$,由范围A∈(30°,90°),利用正弦函数的性质可求S△ABC的范围.
解答 解:(1)∵$B={60°},b=\sqrt{3}$,
∴由余弦定理,可得:3=a2+c2-ac=(a+c)2-3ac,可得:(a+c)2=3ac+3,
又∵3=a2+c2-ac≥2ac-ac=ac,当且仅当a=c时等号成立,
∴(a+c)2=3ac+3≤3×3+3=12,即a+c≤2$\sqrt{3}$,当且仅当a=c时等号成立,
∴a+c的最大值为$2\sqrt{3}$.
(2)∵$B={60°},b=\sqrt{3}$,$\frac{a}{sinA}=\frac{c}{sinC}=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}=2$,
∴S△ABC=$\frac{1}{2}$acsinB
=$\frac{1}{2}×$2sinA×2sinC×$\frac{\sqrt{3}}{2}$
=$\sqrt{3}$sinAsinC
=$\sqrt{3}$sinAsin(120°-A)
=$\sqrt{3}$sinA[$\frac{\sqrt{3}}{2}$cosA+$\frac{1}{2}$sinA]
=$\frac{\sqrt{3}}{2}$sin(2A-30°)+$\frac{\sqrt{3}}{4}$,
∵A∈(30°,90°),可得:2A-30°∈(30°,150°),
∴sin(2A-30°)∈($\frac{1}{2}$,1],可得:S△ABC=$\frac{\sqrt{3}}{2}$sin(2A-30°)+$\frac{\sqrt{3}}{4}$∈$(\frac{{\sqrt{3}}}{2},\frac{{3\sqrt{3}}}{4}]$.
点评 本题主要考查了余弦定理,基本不等式,正弦定理,三角形面积公式,三角函数恒等变换的应用,正弦函数的性质在解三角形中的综合应用,考查了转化思想和数形结合思想,属于中档题.

| A. | y=1 | B. | y=x-1 | C. | y=x+1 | D. | y=x3 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
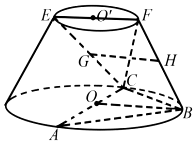 在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′直径,FB是圆台的一条母线.
在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′直径,FB是圆台的一条母线.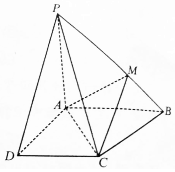 如图,四棱锥P-ABCD中,PA⊥底面ABCD,∠BAD=∠ADC=$\frac{π}{2}$,AB=AD=AP=3,DC=2,点M在PB上,且PM=2MB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,∠BAD=∠ADC=$\frac{π}{2}$,AB=AD=AP=3,DC=2,点M在PB上,且PM=2MB.