题目内容
已知函数f(x)=cos(2x- )+sin2x-cos2x.
)+sin2x-cos2x.
(Ⅰ)求函数f(x)的最小正周期及其图象的对称轴方程;
(Ⅱ)设函数g(x)=[f(x)]2+f(x),求g(x)的值域.
(Ⅰ) 的最小正周期为
的最小正周期为 ,函数图象的对称轴方程为
,函数图象的对称轴方程为 ;
;
(Ⅱ) 的值域为
的值域为 .
.
解析试题分析:(Ⅰ)先利用公式化简得 ,再根据公式得到最小正周期及对称轴方程;(Ⅱ)先化简得
,再根据公式得到最小正周期及对称轴方程;(Ⅱ)先化简得 ,从而可知当
,从而可知当 时,
时, 取得最小值
取得最小值 ,当
,当 时,
时, 取得最大值2, 所以
取得最大值2, 所以 的值域为
的值域为 .
.
试题解析:(Ⅰ)
 . (3分)
. (3分)
 的最小正周期为
的最小正周期为 ,由
,由 得
得
 函数图象的对称轴方程为
函数图象的对称轴方程为 (6分)
(6分)
(Ⅱ)
 (8分)
(8分)
当 时,
时, 取得最小值
取得最小值 ,
,
当 时,
时, 取得最大值2,
取得最大值2,
所以 的值域为
的值域为 . (12分)
. (12分)
考点:1.和角差角、二倍角公式;2.三角函数的性质;3.函数的值域.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
 中,内角
中,内角 所对的边长分别为
所对的边长分别为 ,
, ,
, ,
, .
. 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知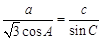 ,
, 的大小;
的大小; ,求
,求 的取值范围.
的取值范围. 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 ,
, .
. 的大小;
的大小;  ,求
,求 的三个内角且向量
的三个内角且向量 与
与 共线.
共线. 的对边分别是
的对边分别是 ,且满足
,且满足 ,试判断
,试判断
 的形状.
的形状. 中,
中, 分别是三个内角
分别是三个内角 的对边.若
的对边.若 ,
, ,
,  的值;
的值; .
. 海里的速度向正北方向航行,
海里的速度向正北方向航行,
 ,求塔高AB.
,求塔高AB.
 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两点,现测得
两点,现测得 ,
, ,
, ,
, ,
, ,试求两景点
,试求两景点