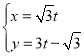题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() ,
,![]() ,且
,且![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() ,点
,点![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作
作![]() 的切线
的切线![]() ,若
,若![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】
(1)依题意,列出方程组,求得![]() ,即可求得椭圆的方程;
,即可求得椭圆的方程;
(2)设![]() :
:![]() ,联立方程组,利用根与系数的关系,求得
,联立方程组,利用根与系数的关系,求得![]() , 结合导数,求得
, 结合导数,求得![]() ,得到
,得到![]() ,求得
,求得![]() 的方程,再利用弦长公式和点到直线的距离公式,表示出三角形
的方程,再利用弦长公式和点到直线的距离公式,表示出三角形![]() ,结合二次函数的性质,即可求解.
,结合二次函数的性质,即可求解.
(1)依题意,椭圆![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() ,且
,且![]() 的离心率为
的离心率为![]() ,可得
,可得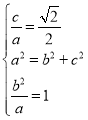 ,解得
,解得![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() ,整理得
,整理得![]() ,则
,则![]() ,
,
由![]() ,可得
,可得![]() ,所以
,所以![]() ,
,
因为![]() ,可得
,可得![]() ,
,
又![]() ,所以
,所以![]() ,即直线
,即直线![]() ,
,
联立 ,整理得
,整理得![]() ,
,
所以![]() ,
,
所以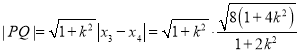 ,
,
又由原点到直线![]() 的距离
的距离![]() ,
,
故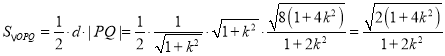 ,
,
设![]() ,则
,则![]() ,
,
代入上式可得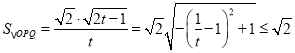 ,
,
当![]() ,即
,即![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
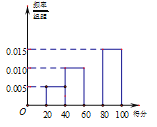
【题目】某央企在一个社区随机采访男性和女性用户各50名,统计他(她)们一天(![]() )使用手机的时间,其中每天使用手机超过6小时(含6小时)的用户称为“手机迷”,否则称其为“非手机迷”,调查结果如下:
)使用手机的时间,其中每天使用手机超过6小时(含6小时)的用户称为“手机迷”,否则称其为“非手机迷”,调查结果如下:
男性用户的频数分布表
男性用户日用时间分组( |
|
|
|
|
|
频数 | 20 | 12 | 8 | 6 | 4 |
女性用户的频数分布表
女性用户日用时间分组( |
|
|
|
|
|
频数 | 25 | 10 | 6 | 8 | 1 |
(1)分别估计男性用户,女性用户“手机迷”的频率;
(2)求男性用户每天使用手机所花时间的中位数;
(3)求女性用户每天使用手机所花时间的平均数与标准差(同一组中的数据用该组区间的中点值作代表).