题目内容
【题目】知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)讨论![]() 的单调性;
的单调性;
(3)若![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() .
.
(2)见解析.
(3)![]() .
.
【解析】分析:(1)根据![]() ,代入得到
,代入得到![]() ,代入
,代入![]() 求得点坐标为
求得点坐标为![]() ;求出导函数,代入
;求出导函数,代入![]() 得到斜率为
得到斜率为![]() ,因而求得切线方程为
,因而求得切线方程为![]() 。
。
(2)根据导函数,对![]() 讨论不同情况下导函数的符号,得到单调区间。
讨论不同情况下导函数的符号,得到单调区间。
(3)根据(2)及恒成立,可得![]() 。构造函数
。构造函数![]() ,根据
,根据![]() 及其在
及其在![]() 上的单调性解关于m的不等式,求得m的取值范围。
上的单调性解关于m的不等式,求得m的取值范围。
详解:(1)当![]() 时,
时,![]() ,
,
![]() ,则
,则![]() ,
,![]() ,
,
故曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(2)![]()
![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,若
时,若![]() ,
,![]() ;若
;若![]() ,
,![]() .
.
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
当![]() 时,若
时,若![]() ,
,![]() ;若
;若![]() ,
,![]() .
.
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(3)∵![]() ,∴由(2)知
,∴由(2)知![]() .
.
设![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() .
.
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,∴
,∴![]() ,
,
故![]() 的取值范围为
的取值范围为![]() .
.

【题目】为了解学生的课外阅读时间情况,某学校随机抽取了50人进行统计分析,把这50人每天阅读的时间(单位:分钟)绘制成频数分布表,如下表所示:
阅读时间 |
|
|
|
|
|
|
人数 | 8 | 10 | 12 | 11 | 7 | 2 |
若把每天阅读时间在60分钟以上(含60分钟)的同学称为“阅读达人”,根据统计结果中男女生阅读达人的数据,制作成如图所示的等高条形图.
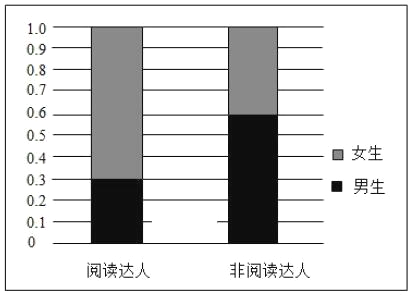
(1)根据抽样结果估计该校学生的每天平均阅读时间(同一组数据用该区间的终点值作为代表);
(2)根据已知条件完成下面的![]() 列联表,并判断是否有99%的把握认为“阅读达人”跟性别有关?
列联表,并判断是否有99%的把握认为“阅读达人”跟性别有关?
男生 | 女生 | 总计 | |
阅读达人 | |||
非阅读达人 | |||
总计 |
附:参考公式![]() ,其中
,其中![]() .
.
临界值表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某单位招聘员工,有![]() 名应聘者参加笔试,随机抽查了其中
名应聘者参加笔试,随机抽查了其中![]() 名应聘者笔试试卷,统计他们的成绩如下表:
名应聘者笔试试卷,统计他们的成绩如下表:
分数段 |
|
|
|
|
|
|
|
人数 | 1 | 3 | 6 | 6 | 2 | 1 | 1 |
若按笔试成绩择优录取![]() 名参加面试,由此可预测参加面试的分数线为( )
名参加面试,由此可预测参加面试的分数线为( )
A. ![]() 分 B.
分 B. ![]() 分 C.
分 C. ![]() 分 D.
分 D. ![]() 分
分
