题目内容
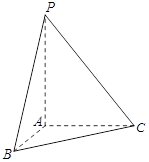
在四棱锥 中,
中, ,
, ,
, 平面
平面 ,
, 为
为  的中点,
的中点, .
.

(1)求四棱锥 的体积
的体积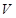 ;
;
(2)若 为
为 的中点,求证:平面
的中点,求证:平面 平面
平面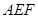 ;
;
(3)求二面角 的大小.
的大小.
 中,
中, ,
, ,
, 平面
平面 ,
, 为
为  的中点,
的中点, .
.
(1)求四棱锥
 的体积
的体积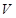 ;
;(2)若
 为
为 的中点,求证:平面
的中点,求证:平面 平面
平面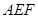 ;
;(3)求二面角
 的大小.
的大小.1)解:在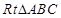 中,
中, ,
,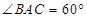 ,∴
,∴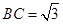 ,
,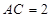 ……1分
……1分
在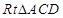 中,
中,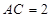 ,
,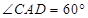 ,∴
,∴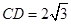 ,
,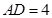 …………2分
…………2分
∴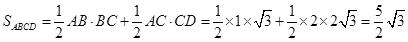 …………3分
…………3分
则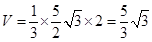 …………………………………………4分
…………………………………………4分
(2)解法一∵ 平面
平面 ,∴
,∴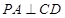 …………………………5分
…………………………5分
又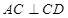 ,
, 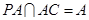 , …………………………6分
, …………………………6分
∴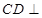 平面
平面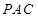 ………………………7分
………………………7分
∵ 、
、 分别为
分别为 、
、 中点,
中点,
∴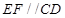 ∴
∴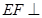 平面
平面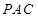 ………………………8分
………………………8分
∵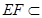 平面
平面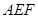 ,∴平面
,∴平面 平面
平面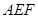 ……9分
……9分
(3)解法一:取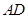 的中点
的中点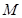 ,连结
,连结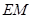 ,则
,则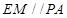 ,
,
∴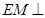 平面
平面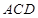 ,过
,过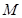 作
作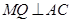 于
于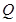 ,连接
,连接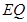 ,…10分
,…10分
∵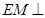 AC,
AC,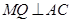 ,且
,且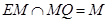 ,∴
,∴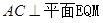 …11分
…11分
则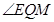 为二面角
为二面角 的平面角。 ……12分
的平面角。 ……12分
∵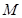 为
为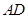 的中点,
的中点,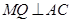 ,
,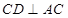 ,
,
∴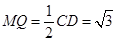 ,又
,又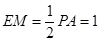 , ……13分
, ……13分
∴ ,故
,故
即二面角 的大小为300……………14分
的大小为300……………14分
(2)解法二:建立如图所示的空间直角坐标系A-xyz ………………5分
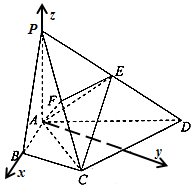
A(0,0,0) B(1,0,0)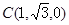
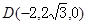
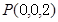
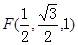
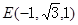 ……6分
……6分
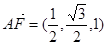 ,
,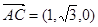 ,
,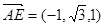 …7分
…7分
设平面AEF的一个法向量为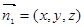
由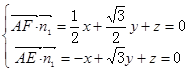 取
取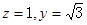 ,得x=1,即
,得x=1,即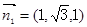 …8分
…8分
又平面PAC的一个法向量为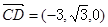 ……9分
……9分
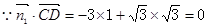 ∴平面
∴平面 平面
平面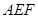 ……10分
……10分
(3)解法二:易知平面ACD的一个法向量为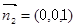 ……11分
……11分
设平面AEF的一个法向量为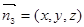
由 ,取
,取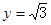 ,得
,得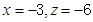 ,
,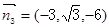 …12分
…12分
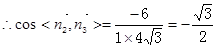 ……13分
……13分
∴结合图形知二面角 的大小为300……………14分
的大小为300……………14分
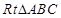 中,
中, ,
,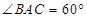 ,∴
,∴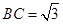 ,
,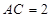 ……1分
……1分在
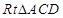 中,
中,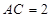 ,
,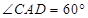 ,∴
,∴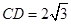 ,
,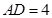 …………2分
…………2分∴
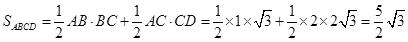 …………3分
…………3分则
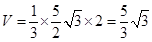 …………………………………………4分
…………………………………………4分(2)解法一∵
 平面
平面 ,∴
,∴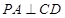 …………………………5分
…………………………5分又
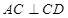 ,
, 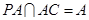 , …………………………6分
, …………………………6分∴
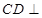 平面
平面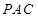 ………………………7分
………………………7分 ∵
 、
、 分别为
分别为 、
、 中点,
中点, ∴
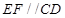 ∴
∴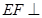 平面
平面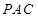 ………………………8分
………………………8分∵
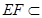 平面
平面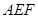 ,∴平面
,∴平面 平面
平面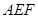 ……9分
……9分
(3)解法一:取
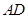 的中点
的中点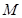 ,连结
,连结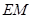 ,则
,则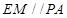 ,
,∴
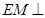 平面
平面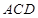 ,过
,过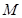 作
作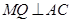 于
于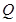 ,连接
,连接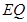 ,…10分
,…10分∵
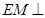 AC,
AC,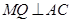 ,且
,且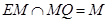 ,∴
,∴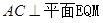 …11分
…11分则
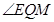 为二面角
为二面角 的平面角。 ……12分
的平面角。 ……12分∵
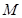 为
为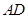 的中点,
的中点,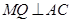 ,
,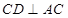 ,
,∴
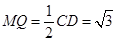 ,又
,又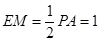 , ……13分
, ……13分∴
 ,故
,故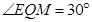
即二面角
 的大小为300……………14分
的大小为300……………14分(2)解法二:建立如图所示的空间直角坐标系A-xyz ………………5分

A(0,0,0) B(1,0,0)
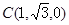
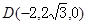
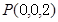
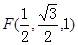
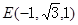 ……6分
……6分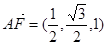 ,
,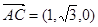 ,
,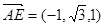 …7分
…7分设平面AEF的一个法向量为
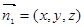
由
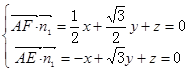 取
取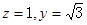 ,得x=1,即
,得x=1,即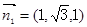 …8分
…8分又平面PAC的一个法向量为
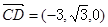 ……9分
……9分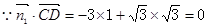 ∴平面
∴平面 平面
平面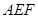 ……10分
……10分(3)解法二:易知平面ACD的一个法向量为
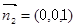 ……11分
……11分设平面AEF的一个法向量为
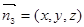
由
 ,取
,取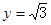 ,得
,得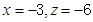 ,
,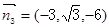 …12分
…12分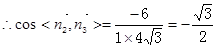 ……13分
……13分∴结合图形知二面角
 的大小为300……………14分
的大小为300……………14分本题考查用分割法求出棱锥的底面积,直线与平面垂直的判定以及求二面角的大小的方法.
(Ⅰ)把四边形面积分成2个直角三角形面积之和,代入棱锥体积公式进行计算.
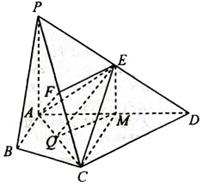
(Ⅱ)先证 CD⊥平面PAC,由三角形中位线的性质得EF∥CD,得到EF⊥平面PAC,从而证得平面PAC⊥平面AEF.
(Ⅲ)由三垂线定理作出∠EQM为二面角E-AC-D的平面角,并证明之,解直角三角形EQM,求出∠EQM的大小.
(Ⅰ)把四边形面积分成2个直角三角形面积之和,代入棱锥体积公式进行计算.
(Ⅱ)先证 CD⊥平面PAC,由三角形中位线的性质得EF∥CD,得到EF⊥平面PAC,从而证得平面PAC⊥平面AEF.
(Ⅲ)由三垂线定理作出∠EQM为二面角E-AC-D的平面角,并证明之,解直角三角形EQM,求出∠EQM的大小.

练习册系列答案
相关题目
 中,底面
中,底面 是直角梯形,
是直角梯形,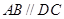 ,
,
 ,
,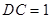 ,
, ,
, 平面
平面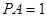 .
. 平面
平面 ;
; 平面
平面 ;
;  是
是 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积.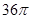 , 则此正方体的表面积是
, 则此正方体的表面积是


 中,
中,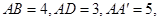 ∠
∠ ,
, =∠
=∠ ,则
,则 等于( )
等于( )





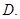

 ,且
,且 ,以BD为折线,把
,以BD为折线,把 折起,使平面
折起,使平面 ,连AC。
,连AC。
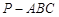 ,
,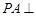 平面
平面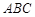 ,
,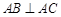 ,
,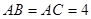 ,
,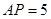 .
.
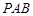 (及其内部)绕
(及其内部)绕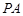 所在直线旋转一周形成一几何体,求该几何体的体积
所在直线旋转一周形成一几何体,求该几何体的体积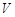 ;
; 的余弦值.
的余弦值. 的8个顶点都在体积为
的8个顶点都在体积为 的球面上,若
的球面上,若 ,则
,则 __________.
__________.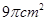 ,且它的侧面展开图是一个半圆,则圆锥的底面半径为
,且它的侧面展开图是一个半圆,则圆锥的底面半径为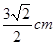

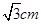
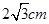 ()
()