题目内容
(本小题满分12分)如图,已知四棱锥 中,底面
中,底面 是直角梯形,
是直角梯形,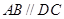 ,
,

 ,
,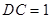 ,
, ,
, 平面
平面 ,
,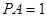 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)若 是
是 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积.
 中,底面
中,底面 是直角梯形,
是直角梯形,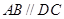 ,
,
 ,
,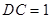 ,
, ,
, 平面
平面 ,
,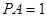 .
.(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求证:
 平面
平面 ;
; (Ⅲ)若
 是
是 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积.(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)

本试题主要是考查了立体几何中线面平行和线面垂直的判定定理的运用,以及棱锥的体积公式计算的综合问题。
(1)因为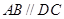 ,结合线面平行的判定定理得到结论。
,结合线面平行的判定定理得到结论。
(2)根据在直角梯形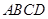 中,过
中,过 作
作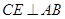 于点
于点 ,
,
则四边形 为矩形,∴
为矩形,∴ ,进而分析得到
,进而分析得到 是解决该试题的关键,
是解决该试题的关键,
(3)∵ 是
是 中点,∴
中点,∴ 到面
到面 的距离是
的距离是 到面
到面 距离的一半,那么利用底面积和高得到体积。
距离的一半,那么利用底面积和高得到体积。
证明:(Ⅰ)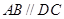 …………… 1分
…………… 1分
又 平面
平面 …………… 2分
…………… 2分
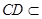 平面
平面 …………… 3分
…………… 3分
∴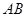 ∥平面
∥平面 …………… 4分
…………… 4分
(Ⅱ)在直角梯形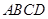 中,过
中,过 作
作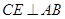 于点
于点 ,
,
则四边形 为矩形,∴
为矩形,∴ ………… 5分
………… 5分
又 ,∴
,∴ ,在
,在 中,
中, ∴
∴ ,∴
,∴
则 ,
, ∴
∴ ………… 7分
………… 7分
又 平面
平面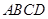 , ∴
, ∴ ………… 8分
………… 8分
 ∴
∴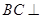 平面
平面 …………… 9分
…………… 9分
(Ⅲ)∵ 是
是 中点,∴
中点,∴ 到面
到面 的距离是
的距离是 到面
到面 距离的一半……… 10分
距离的一半……… 10分
 …………… 12分
…………… 12分
(1)因为
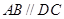 ,结合线面平行的判定定理得到结论。
,结合线面平行的判定定理得到结论。(2)根据在直角梯形
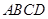 中,过
中,过 作
作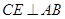 于点
于点 ,
,则四边形
 为矩形,∴
为矩形,∴ ,进而分析得到
,进而分析得到 是解决该试题的关键,
是解决该试题的关键,(3)∵
 是
是 中点,∴
中点,∴ 到面
到面 的距离是
的距离是 到面
到面 距离的一半,那么利用底面积和高得到体积。
距离的一半,那么利用底面积和高得到体积。证明:(Ⅰ)
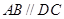 …………… 1分
…………… 1分又
 平面
平面 …………… 2分
…………… 2分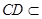 平面
平面 …………… 3分
…………… 3分∴
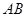 ∥平面
∥平面 …………… 4分
…………… 4分(Ⅱ)在直角梯形
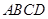 中,过
中,过 作
作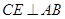 于点
于点 ,
,则四边形
 为矩形,∴
为矩形,∴ ………… 5分
………… 5分又
 ,∴
,∴ ,在
,在 中,
中, ∴
∴ ,∴
,∴
则
 ,
, ∴
∴ ………… 7分
………… 7分又
 平面
平面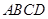 , ∴
, ∴ ………… 8分
………… 8分 ∴
∴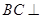 平面
平面 …………… 9分
…………… 9分(Ⅲ)∵
 是
是 中点,∴
中点,∴ 到面
到面 的距离是
的距离是 到面
到面 距离的一半……… 10分
距离的一半……… 10分 …………… 12分
…………… 12分 
练习册系列答案
相关题目
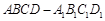 的棱长为1,
的棱长为1,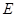 为线段
为线段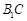 上的一点,则三棱锥
上的一点,则三棱锥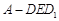 的体积为 .
的体积为 .
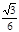 B.arccos
B.arccos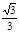 D.arccos
D.arccos ,那么该三棱柱的体积为
,那么该三棱柱的体积为
 中,
中, ,
, ,
, 平面
平面 ,
, 为
为  的中点,
的中点, .
.
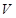 ;
; 为
为 的中点,求证:平面
的中点,求证:平面 平面
平面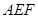 ;
; 的大小.
的大小. 的棱长都为2,
的棱长都为2, 为
为 的中点,则
的中点,则 与面GEF成角的正弦值是( )
与面GEF成角的正弦值是( )




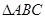 沿
沿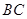 边上的高
边上的高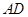 折成直二面角
折成直二面角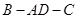 ,则三棱锥
,则三棱锥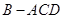 的外接球的表面积为 _________
的外接球的表面积为 _________ ,则三棱锥的体积与其外接球体积之比是 。
,则三棱锥的体积与其外接球体积之比是 。