题目内容
设函数f(x)=
,则函数y=f(x)-(x2+1)的零点个数为( )
|
| A、1 | B、2 | C、3 | D、4 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:将问题转化为y=f(x),y=x2+1的交点问题,画出图象读出即可.
解答:
 解:令y=f(x)-(x2+1)=0,
解:令y=f(x)-(x2+1)=0,
∴f(x)=x2+1,
画出y=f(x),y=x2+1的图象,
如图示:
∴函数有2个交点,
故选:B.
 解:令y=f(x)-(x2+1)=0,
解:令y=f(x)-(x2+1)=0,∴f(x)=x2+1,
画出y=f(x),y=x2+1的图象,
如图示:
∴函数有2个交点,
故选:B.
点评:本题考查了函数的交点问题,考查了转化思想,是一道基础题.

练习册系列答案
相关题目
函数f(x)=lgsin(
-2x)的单调递减区间是( ),其中k∈Z.
| π |
| 3 |
A、(kπ+
| ||||
B、(kπ+
| ||||
C、(kπ-
| ||||
D、(kπ+
|

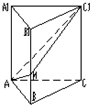 如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=
如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=