题目内容
已知x2+y2=1,求(x-2)2+(y-3)2的取值范围.
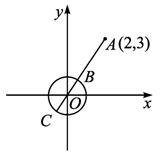
分析：本题若通过三角换元x=cosα,y=sinα把问题转化为三角问题运算较繁，若换个角度x2+y2=1可看成单位圆,而(x-2)2+(y-3)2可看成是定点(2，3)与单位圆上点的距离的平方，数形结合问题易于解决.
解：定点A(2，3),|AO|=
.∴|AB|=
-1,|AC|=
+1.
故(x-2)2+(y-3)2的取值范围是［(
-1)2，(
+1)2］.
练习册系列答案
相关题目
已知x2+y2=1，x＞0．y＞0，且loga(1+x)=m，loga
=n，则logay等于（ ）
| 1 |
| 1-x |
| A、m+n | ||
| B、m-n | ||
C、
| ||
D、
|
已知x2+y2=1，则（1-xy）（1+xy）有（ ）
A、最大值
| ||
B、最大值1，最小值
| ||
C、最小值
| ||
| D、最大值1，无最小值 |