题目内容
(
北京海淀模拟)如下图,已知平行六面体 的底面为正方形,
的底面为正方形, 、O分别为上、下底面的中心,且
、O分别为上、下底面的中心,且 在底面ABCD上的射影是O.
在底面ABCD上的射影是O.

(1)
求证:平面 ⊥平面ABCD;
⊥平面ABCD;
(2)
若点E,F分别在棱 ,BC上,且
,BC上,且 ,问点F在何处时,EF⊥AD?
,问点F在何处时,EF⊥AD?
(3)
若 ,求二面角C-
,求二面角C- -B的大小(用反三角函数表示).
-B的大小(用反三角函数表示).
答案:略
解析:
解析:
|
解析: (1)连结AC,BD,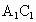 ,则O为AC,BD的交点, ,则O为AC,BD的交点,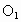 为 为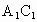 , ,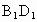 的交点.由平行六面体的性质知: 的交点.由平行六面体的性质知: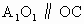 且 且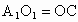 , ,
∴四边形 ∴ 又∵ ∴ 又∵ ∴平面 (2) 作EH⊥平面ABCD,垂足为H,则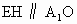 ,点H在直线AC上,且EF在平面ABCD上的射影为HF.由三垂线定理及其逆定理, ,点H在直线AC上,且EF在平面ABCD上的射影为HF.由三垂线定理及其逆定理,
知 ∵ 从而 CH=2AH.又∵HF∥AB,∴ CF=2BF,从而 . .
∴当 F为BC的三等分点(靠近B)时,有EF⊥AD.(2) 过点O作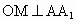 ,垂足为M,连结BM. ,垂足为M,连结BM.
∵ 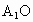 ⊥平面ABCD, ⊥平面ABCD,
∴ 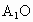 ⊥OB. ⊥OB.
又∵ OB⊥OA.∴OB⊥平面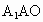 ,由三垂线定理得 ,由三垂线定理得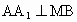 . .
∴∠ OMB为二面角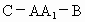 的平面角, 的平面角,
在 Rt△AMB中,∠MAB=60°,∴ 又∵ ∴ ∴二面角 |

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
(2007
北京海淀模拟)函数y=kx+b,其中k,b(k≠0)是常数,其图象是一条直线,称这个函数为线性函数,对于非线性可导函数f(x),在点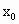 附近一点x的函数值f(x),可以用如下方法求其近似代替值:
附近一点x的函数值f(x),可以用如下方法求其近似代替值: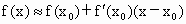 .利用这一方法,
.利用这一方法,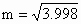 的近似代替值
的近似代替值
[
]|
A .大于m |
B .小于m |
|
C .等于m |
D .与m的大小关系无关 |
 为平行四边形,
为平行四边形, .
. ⊥平面
⊥平面 平面
平面 平面
平面 ,
, 平面
平面
 .
. ,∴
,∴ .
. ,∴
,∴ ,
, .
. .
.