题目内容
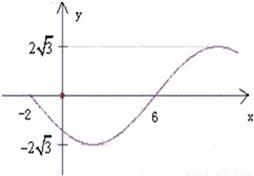
如图,根据函数的图象,求函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的解析式.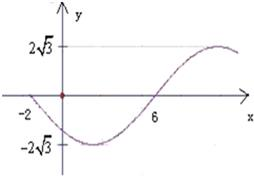
分析:根据图象的最高点确定三角函数的振幅,根据半个周期的长度,确定函数的周期和ω的值,根据图象过一个点,把这个点代入函数的解析式,求出φ的值,最后写出函数的解析式.
解答:解:由图象的最高点可以看出A=2
,T=16,即16ω=2π
∴ω=
∴y=2
sin(
x+∅)
又∵点(2,-2
)在曲线上,代入得 2
sin(
×2+∅)=-2
∴sin(
+∅)=-1
∴
+∅=2kπ-
∴φ=2kπ-
k∈z
又∵|φ|<π
∴φ=-
∴函数解析式为y=2
sin(
x-
)
| 3 |
∴ω=
| π |
| 8 |
∴y=2
| 3 |
| π |
| 8 |
又∵点(2,-2
| 3 |
| 3 |
| π |
| 8 |
| 3 |
∴sin(
| π |
| 4 |
∴
| π |
| 4 |
| π |
| 2 |
∴φ=2kπ-
| 3π |
| 4 |
又∵|φ|<π
∴φ=-
| 3π |
| 4 |
∴函数解析式为y=2
| 3 |
| π |
| 8 |
| 3π |
| 4 |
点评:本题考查根据函数的图象确定函数的解析式,本题是一个基础题,在解题过程中注意φ的值是最难确定的,注意使用代入点的方法,或者是用五点法来确定.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
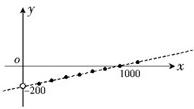 17、某计算机集团公司生产某种型号计算机的固定成本为200万元,生产每台计算机的可变成本为3000元,利润y(万元) 关于总产量x(台)的函数的图象如图所示.
17、某计算机集团公司生产某种型号计算机的固定成本为200万元,生产每台计算机的可变成本为3000元,利润y(万元) 关于总产量x(台)的函数的图象如图所示.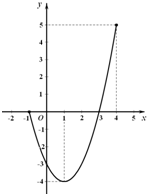 二次函数y=f(x)的图象的一部分如图所示.
二次函数y=f(x)的图象的一部分如图所示.