Question

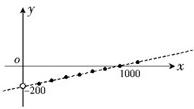17、某计算机集团公司生产某种型号计算机的固定成本为200万元，生产每台计算机的可变成本为3000元，利润y（万元） 关于总产量x（台）的函数的图象如图所示．
（1）根据图象写出y（万元） 关于总产量x（台）的函数关系式．
（2）求出每台计算机的售价．

Answer 1

分析：（1）根据图象函数是一次函数模型，可设y=kx+b，再由过（0，200），（1000，0）解得函数模型．
（2）设每台售价m万元，则利润为：mx-（200+0.3x）又因为利润为：0.2x-200，建立方程解得m．

解答：解：（1）如图所示：设y=kx+b，
∵函数过（0，200），（1000，0）
代入上式得：k=0.2，b=-200
∴y=0.2x-200（x∈N*）
（2）设每台售价m万元，根据题意有：
mx-（200+0.3x）=0.2x-200，
∴m=0.5
答：（1）y关于x的函数关系式为y=0.2x-200（x∈N*）
（2）每台计算机售价0.5万元（14分）

点评：本题主要考查函数模型的建立与应用，主要涉及一次函数，一次方程，数形结合法等．