题目内容
在△ABC中,b2-bc-2c2=0,a=
,cosA=
,则△ABC的面积为( )
| 6 |
| 7 |
| 8 |
分析:由已知的等式分解因式,求出b与c的关系,用c表示出b,然后根据余弦定理表示出cosA,把a与cosA的值代入即可得到b与c的关系式,将表示出的含c的式子代入即可得到关于b的方程,求出方程的解即可得到b的值,从而求得c的值,即可求得△ABC的面积.
解答:解:由b2-bc-2c2=0因式分解得:(b-2c)(b+c)=0,解得:b=2c,b=-c(舍去).
又根据余弦定理得:cosA=
=
=
,化简得:4b2+4c2-24=7bc,
将c=
代入得:4b2+b2-24=
b2,即b2=16,解得:b=4或b=-4(舍去),则b=4,故c=2.
由 cosA=
可得 sinA=
,故△ABC的面积为
bc•sinA=
,
故选B.
又根据余弦定理得:cosA=
| b2+c 2 -a 2 |
| 2bc |
| b2+c 2 -6 |
| 2bc |
| 7 |
| 8 |
将c=
| b |
| 2 |
| 7 |
| 2 |
由 cosA=
| 7 |
| 8 |
| ||
| 8 |
| 1 |
| 2 |
| ||
| 2 |
故选B.
点评:此题考查了余弦定理,及等式的恒等变形.要求学生熟练掌握余弦定理的特征及等式的恒等变换.由已知等式因式分解得到b与c的关系式是本题的突破点,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
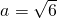 ,
, ,则△ABC的面积为
,则△ABC的面积为

