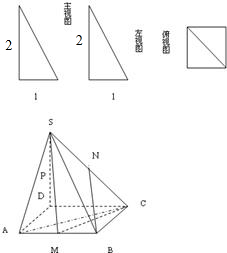
题目内容
一个多面体的三视图和直观图如图所示,其中M,N分别是AB,AC的中点,G是DF上的一个动点,且DG=λDF(0<λ≤1).

(1)求证:对任意的λ∈(0,1),都有GN⊥AC;
(2)当λ=
时,求证:AG∥平面FMC.

(1)求证:对任意的λ∈(0,1),都有GN⊥AC;
(2)当λ=
| 1 |
| 2 |

证明:(1)由题意知,该几何体是一个三棱柱,且CD⊥DF,AD⊥DF,AD⊥CD,DF=AD=DC=a,
如图,连接BD,
∵N为AC与BD的交点,且AC⊥BD.
∴FD⊥平面ABCD,
∵G为FD上的点,∴GD⊥平面ABCD,
∵AC?平面ABCD,∴GD⊥AC,
∵BD∩GD=D,∴AC⊥平面GDN,
∵GN?平面GND,∴AC⊥GN.
(2)当λ=
| 1 |
| 2 |
如图,取DC的中点S,连接AS,CS,
∵M是AB的中点,∴AS∥MC,GS∥FG,
∵AS∩GS=S,FC∩CM=C,∴平面AGS∥平面FMC,
∵AG?平面AGS,∴AG∥平面FMC.

练习册系列答案
相关题目
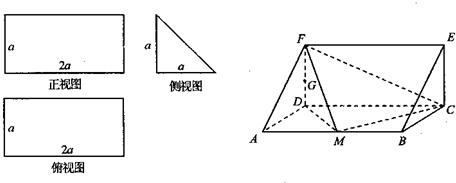
 一个多面体的三视图和直观图如图所示,其中正视图和俯视图均为矩形,侧视图为直角三角形,M是AB的中点.
一个多面体的三视图和直观图如图所示,其中正视图和俯视图均为矩形,侧视图为直角三角形,M是AB的中点.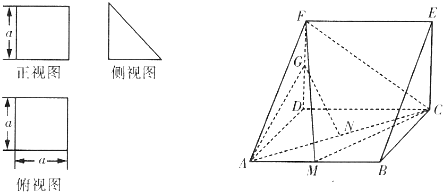
 (2012•香洲区模拟)一个多面体的三视图和直观图如下:
(2012•香洲区模拟)一个多面体的三视图和直观图如下: