题目内容
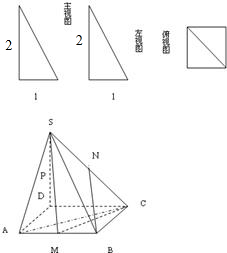
 一个多面体的三视图和直观图如图所示,其中正视图和俯视图均为矩形,侧视图为直角三角形,M是AB的中点.
一个多面体的三视图和直观图如图所示,其中正视图和俯视图均为矩形,侧视图为直角三角形,M是AB的中点.(1)求证:CM⊥平面FDM;
(2)求二面角F-CM-D的正切值.
分析:(1)利用勾股定理、线面垂直的判定定理和性质定理即可证明;
(2)利用(1)的有关结论及二面角的定义可知∠FMD即为二面角F-CM-D的平面角,在Rt△FDM中利用正切函数即可求出.
(2)利用(1)的有关结论及二面角的定义可知∠FMD即为二面角F-CM-D的平面角,在Rt△FDM中利用正切函数即可求出.
解答:解:(1)证明:由正视图和俯视图均为矩形,侧视图为直角三角形,∴FD⊥DC,FD⊥AD,
∵AD∩DC=D,∴FD⊥平面ABCD,∴FD⊥CM.
∵AD=AM=MB=BC=a,∠DAM=∠CBM=90°,
∴DM=MC=
a,
∵CD=2a,∴DM2+CM2=CD2.
∴CM⊥DM.
又∵FD∩DM=D,∴CM⊥平面FDM.
(2)由(1)可知:CM⊥DM,CM⊥FM,∴∠FMD即为二面角F-CM-D的平面角.
由(1)可知:FD⊥平面ABCD,∴FD⊥DM.
在Rt△FDM中,tan∠FMD=
=
=
.
∵AD∩DC=D,∴FD⊥平面ABCD,∴FD⊥CM.
∵AD=AM=MB=BC=a,∠DAM=∠CBM=90°,
∴DM=MC=
| 2 |
∵CD=2a,∴DM2+CM2=CD2.
∴CM⊥DM.
又∵FD∩DM=D,∴CM⊥平面FDM.
(2)由(1)可知:CM⊥DM,CM⊥FM,∴∠FMD即为二面角F-CM-D的平面角.
由(1)可知:FD⊥平面ABCD,∴FD⊥DM.
在Rt△FDM中,tan∠FMD=
| FD |
| DM |
| a | ||
|
| ||
| 2 |
点评:熟练掌握勾股定理、线面垂直的判定定理和性质定理、二面角的平面角的定义及作法、正切函数的定义是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
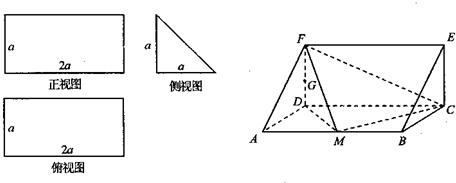
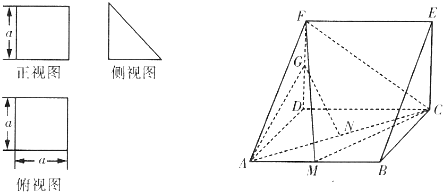
 (2012•香洲区模拟)一个多面体的三视图和直观图如下:
(2012•香洲区模拟)一个多面体的三视图和直观图如下: