题目内容
7.设函数f(x)是R上的偶函数,在[0,+∞)上为增函数,又f(1)=0,则函数F(x)=f(x)•xln$\frac{e}{\sqrt{3}+1}$的图象在x轴上方时x的取值范围是( )| A. | (-1,0)∪(1,+∞) | B. | (-∞,-1)∪(0,1) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
分析 根据函数的奇偶性和单调性之间的关系,将不等式进行转化,即可得到不等式的解集.
解答 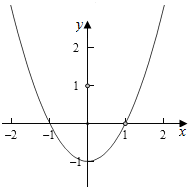 解:∵偶函数f(x)在[0,+∞)上为增函数,f(1)=0,
解:∵偶函数f(x)在[0,+∞)上为增函数,f(1)=0,
∴对应的图象如图:
∵ln$\frac{e}{\sqrt{3}+1}$<0,
∴由F(x)=f(x)•xln$\frac{e}{\sqrt{3}+1}$>0,
得f(x)•x<0,
即$\left\{\begin{array}{l}{x>0}\\{f(x)<0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)>0}\end{array}\right.$,
即0<x<1或x<-1,
即不等式的解集为(-∞,-1)∪(0,1),
故选:B.
点评 本题主要考查不等式的解法,利用函数的奇偶性和单调性之间的关系是解决本题的关键,综合考查函数性质的应用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
17.阳澄湖大闸蟹的上市规格为:特级雄蟹≥200g,雄蟹≥150g,一级雄蟹≥150g,雌蟹≥125g;二级雄蟹≥125g,雌蟹≥100g.现从某批上市的大闸蟹中随机抽取100只,得到的数据如下:
(1)根据雌雄按分层抽样的方法从这100只大闸蟹中抽取20只,若雌蟹有8只,求a,b的值;
(2)按样本估计总体的方法从这批上市的大闸蟹中有放回地随机抽取3只,记特级雄蟹的只数为X,求X的数学期望.
| 雄蟹 | 雌蟹 | |||||
| 等级 | 特级 | 一级 | 二级 | 特级 | 一级 | 二级 |
| 只数 | 30 | a | 10 | 20 | 10 | b |
(2)按样本估计总体的方法从这批上市的大闸蟹中有放回地随机抽取3只,记特级雄蟹的只数为X,求X的数学期望.
17.表面积为8$\sqrt{3}$的正四面体的外接球的表面积为( )
| A. | 4$\sqrt{3}$π | B. | 12π | C. | 8π | D. | 4$\sqrt{6}$π |