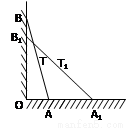题目内容
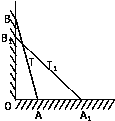如图，长为4米的直竹竿AB两端分别在水平地面和墙上（地面与墙面垂直），T为AB中点，∠OAB=75°，当竹竿滑动到A1B1位置时，∠O1A1B=45°，竹竿在滑动时中点T也沿着某种轨迹运动到T1点，则T运动的路程是| π |
| 3 |
| π |
| 3 |
分析：连接OT、OT1，确定∠TOT1=90°-15°-45°=30°，利用弧长公式，即可得出结论．
解答：
解：连接OT、OT1，
∵∠OAB=75°，∠O1A1B=45°，
∴∠AOT=∠TAO=15°，∠T1OB=∠T1BO=45°，
∴∠TOT1=90°-15°-45°=30°，
∵竹竿在滑动时中点T与O的距离始终等于AB的一半，
所以点T一直在以原点为圆心，以2为半径的圆弧上，转过的圆心角为
∴T运动的路程是
×2=
故答案为：
解：连接OT、OT1，∵∠OAB=75°，∠O1A1B=45°，
∴∠AOT=∠TAO=15°，∠T1OB=∠T1BO=45°，
∴∠TOT1=90°-15°-45°=30°，
∵竹竿在滑动时中点T与O的距离始终等于AB的一半，
所以点T一直在以原点为圆心，以2为半径的圆弧上，转过的圆心角为
| π |
| 6 |
∴T运动的路程是
| π |
| 6 |
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题考查了弧长的计算，解答本题的关键是确定点T行走路径，属于中档题．
练习册系列答案
相关题目
（2013•湖南）某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获Y（单位：kg）与它的“相近”作物株数X之间的关系如下表所示：
，当竹竿滑动到A1B1位置时，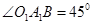
，竹竿在滑动时中点T也沿着某种轨迹运动到T1点，则T运动的路程是_________米.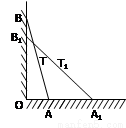
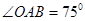，当竹竿滑动到A1B1位置时，
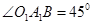，竹竿在滑动时中点T也沿着某种轨迹运动到T1点，则T运动的路程是_________米.