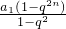Question

在等比数列该数列{a_n}中，公比为q（q≠±1），则数列a₂，a₄，a₆，…，a_2n的前n项和T_n为：（　　）

• A、

  a1(1-q2n)

  1-q2

• B、

  a2(1-q2n)

  1-q2

• C、

  a1(1-qn)

  1-q2

• D、

  a2(1-qn)

  1-q2

Answer 1

分析：依题意可知数列a₂，a₄，a₆，…，a_2n的是以q²为公比a₂为首项的等比数列，进而根据等比数列的求和公式可得答案．

解答：解：依题意可知数列a₂，a₄，a₆，…，a_2n的是以q²为公比a₂为首项的等比数列，
进而根据等比数列的求和公式可得T_n=

a2(1-q2n)

1-q2

故选B

点评：本题主要考查了等比数列的前n项和．属基础题．