题目内容
17.已知向量$\overrightarrow{m}$=(cosx,sinx),$\overrightarrow{n}$=(2$\sqrt{2}$+sinx,2$\sqrt{2}$-cosx),函数f(x)=$\overrightarrow{m}$$•\overrightarrow{n}$,x∈R.(Ⅰ)求函数f(x)的最大值;
(Ⅱ)若x∈(-$\frac{3π}{2}$,-π)且f(x)=1,求cos(x+$\frac{5π}{12}$)的值.
分析 (Ⅰ)由向量的数量积和三角函数公式可得f(x)=4sin(x+$\frac{π}{4}$),可得最大值;
(Ⅱ)由题意可得sin(x+$\frac{π}{4}$)=$\frac{1}{4}$,由x范围和同角三角函数基本关系可得cos(x+$\frac{π}{4}$)=-$\frac{\sqrt{15}}{4}$,整体代入cos(x+$\frac{5π}{12}$)=cos[(x+$\frac{π}{4}$)+$\frac{π}{6}$]=$\frac{\sqrt{3}}{2}$cos(x+$\frac{π}{4}$)-$\frac{1}{2}$sin(x+$\frac{π}{4}$),计算可得.
解答 解:(Ⅰ)∵$\overrightarrow{m}$=(cosx,sinx),$\overrightarrow{n}$=(2$\sqrt{2}$+sinx,2$\sqrt{2}$-cosx),
∴f(x)=$\overrightarrow{m}$$•\overrightarrow{n}$=cosx(2$\sqrt{2}$+sinx)+sinx(2$\sqrt{2}$-cosx)
=2$\sqrt{2}$(sinx+cosx)=4sin(x+$\frac{π}{4}$),
∴函数f(x)的最大值为4;
(Ⅱ)∵f(x)=4sin(x+$\frac{π}{4}$)=1,∴sin(x+$\frac{π}{4}$)=$\frac{1}{4}$,
∵x∈(-$\frac{3π}{2}$,-π),∴x+$\frac{π}{4}$∈(-$\frac{5π}{4}$,-$\frac{3π}{4}$),
∴cos(x+$\frac{π}{4}$)=-$\frac{\sqrt{15}}{4}$,
∴cos(x+$\frac{5π}{12}$)=cos[(x+$\frac{π}{4}$)+$\frac{π}{6}$]=$\frac{\sqrt{3}}{2}$cos(x+$\frac{π}{4}$)-$\frac{1}{2}$sin(x+$\frac{π}{4}$)
=-$\frac{\sqrt{15}}{4}$×$\frac{\sqrt{3}}{2}$-$\frac{1}{4}×\frac{1}{2}$=-$\frac{3\sqrt{5}+1}{8}$
点评 本题考查三角函数恒等变换,涉及向量的运算和和差角的三角函数,属中档题.

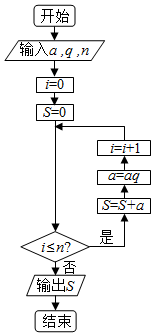
| A. | a+aq+…+aqn-1 | B. | $\frac{{a(1-{q^n})}}{1-q}$ | C. | a+aq+…+aqn | D. | $\frac{{a(1-{q^{n+1}})}}{1-q}$ |

| A. | {2} | B. | {1,2,-1,-2} | C. | {1,-1} | D. | {2,-2} |

| A. | 18 | B. | 50 | C. | 78 | D. | 306 |