题目内容
双曲线的中心在坐标原点O,焦点在x轴上,过双曲线右焦点且斜率为 的直线交双曲线于P、Q两点.若OP⊥OQ,|PQ|=4,求双曲线的方程.
的直线交双曲线于P、Q两点.若OP⊥OQ,|PQ|=4,求双曲线的方程.
 的直线交双曲线于P、Q两点.若OP⊥OQ,|PQ|=4,求双曲线的方程.
的直线交双曲线于P、Q两点.若OP⊥OQ,|PQ|=4,求双曲线的方程.解答见解析.
本小题考查双曲线性质,两点距离公式,两直线垂直条件,代数二次方程等基本知识,以及综合分析能力.满分12分.
解法一:设双曲线的方程为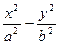 =1.
=1.
依题意知,点P,Q的坐标满足方程组
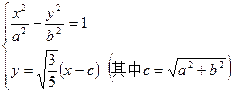 将②式代入①式,整理得(5b2-3a2)x2+6a2cx-(3a2c2+5a2b2)=0. ③ ——3分
将②式代入①式,整理得(5b2-3a2)x2+6a2cx-(3a2c2+5a2b2)=0. ③ ——3分
设方程③的两个根为x1,x2,若5b2-3a2=0,则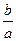 =
= ,即直线②与双曲线①的两条渐近线中的一条平行,故与双曲线只能有一个交点同,与题设矛盾,所以5b2-3a2≠0.
,即直线②与双曲线①的两条渐近线中的一条平行,故与双曲线只能有一个交点同,与题设矛盾,所以5b2-3a2≠0.
根据根与系数的关系,有
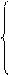
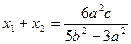 ④
④
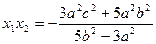 ⑤ ——6分
⑤ ——6分
由于P、Q在直线y= (x-c)上,可记为P (x1,
(x-c)上,可记为P (x1, (x1-c)),Q (x2,
(x1-c)),Q (x2, (x2-c)).
(x2-c)).
由OP⊥OQ得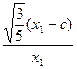 ·
·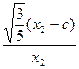 =-1,
=-1,
整理得3c(x1+x2)-8x1x2-3c2=0. ⑥
将④,⑤式及c2=a2+b2代入⑥式,并整理得3a4+8a2b2-3b4=0,即(a2+3b2)(3a2-b2)=0.
因为 a2+3b2≠0,解得b2=3a2,所以 c=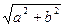 =2a. ——8分
=2a. ——8分
由|PQ|=4,得(x2-x1)2=[ (x2-c)-
(x2-c)- (x1-c)]2=42.
(x1-c)]2=42.
整理得(x1+x2)2-4x1x2-10=0. ⑦
将④,⑤式及b2=3a2,c=2a代入⑦式,解得a2=1. ——10分
将a2 =1代入b2=3a2得 b2=3.
故所求双曲线方程为x2-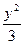 =1. ——12分
=1. ——12分
解法二:④式以上同解法一. ——4分
解方程③得x1=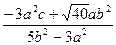 ,x2=
,x2=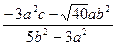 ④ ——6分
④ ——6分
由于P、Q在直线y= (x-c)上,可记为P (x1,
(x-c)上,可记为P (x1, (x1-c)),Q (x2,
(x1-c)),Q (x2, (x2-c)).
(x2-c)).
由OP⊥OQ,得x1 x2+ (x1-c)·
(x1-c)· (x2-c)=0. ⑤
(x2-c)=0. ⑤
将④式及c2=a2b2代入⑤式并整理得 3a4+8a2b2-3b4=0,
即 (a2+3b2)(3a2-b2)=0.因a2+3b2≠0,解得b2=3a2. ——8分
由|PQ|=4,得(x2-x1)2+[ (x2-c)-
(x2-c)- (x1-c)]2=42.
(x1-c)]2=42.
即 (x2-x1)2=10. ⑥
将④式代入⑥式并整理得(5b2-3a2)2-16a2b4=0. ——10分
将b2=3a2代入上式,得a2=1,将a2=1代入b2=3a2得b2=3.
故所求双曲线方程为x2-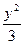 =1. ——12分
=1. ——12分
解法一:设双曲线的方程为
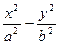 =1.
=1.依题意知,点P,Q的坐标满足方程组
|
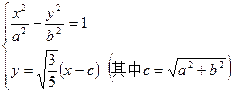 将②式代入①式,整理得(5b2-3a2)x2+6a2cx-(3a2c2+5a2b2)=0. ③ ——3分
将②式代入①式,整理得(5b2-3a2)x2+6a2cx-(3a2c2+5a2b2)=0. ③ ——3分设方程③的两个根为x1,x2,若5b2-3a2=0,则
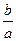 =
= ,即直线②与双曲线①的两条渐近线中的一条平行,故与双曲线只能有一个交点同,与题设矛盾,所以5b2-3a2≠0.
,即直线②与双曲线①的两条渐近线中的一条平行,故与双曲线只能有一个交点同,与题设矛盾,所以5b2-3a2≠0.根据根与系数的关系,有
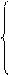
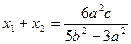 ④
④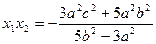 ⑤ ——6分
⑤ ——6分由于P、Q在直线y=
 (x-c)上,可记为P (x1,
(x-c)上,可记为P (x1, (x1-c)),Q (x2,
(x1-c)),Q (x2, (x2-c)).
(x2-c)).由OP⊥OQ得
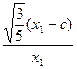 ·
·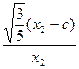 =-1,
=-1,整理得3c(x1+x2)-8x1x2-3c2=0. ⑥
将④,⑤式及c2=a2+b2代入⑥式,并整理得3a4+8a2b2-3b4=0,即(a2+3b2)(3a2-b2)=0.
因为 a2+3b2≠0,解得b2=3a2,所以 c=
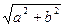 =2a. ——8分
=2a. ——8分由|PQ|=4,得(x2-x1)2=[
 (x2-c)-
(x2-c)- (x1-c)]2=42.
(x1-c)]2=42.整理得(x1+x2)2-4x1x2-10=0. ⑦
将④,⑤式及b2=3a2,c=2a代入⑦式,解得a2=1. ——10分
将a2 =1代入b2=3a2得 b2=3.
故所求双曲线方程为x2-
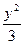 =1. ——12分
=1. ——12分解法二:④式以上同解法一. ——4分
解方程③得x1=
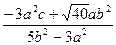 ,x2=
,x2=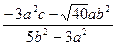 ④ ——6分
④ ——6分由于P、Q在直线y=
 (x-c)上,可记为P (x1,
(x-c)上,可记为P (x1, (x1-c)),Q (x2,
(x1-c)),Q (x2, (x2-c)).
(x2-c)).由OP⊥OQ,得x1 x2+
 (x1-c)·
(x1-c)· (x2-c)=0. ⑤
(x2-c)=0. ⑤将④式及c2=a2b2代入⑤式并整理得 3a4+8a2b2-3b4=0,
即 (a2+3b2)(3a2-b2)=0.因a2+3b2≠0,解得b2=3a2. ——8分
由|PQ|=4,得(x2-x1)2+[
 (x2-c)-
(x2-c)- (x1-c)]2=42.
(x1-c)]2=42.即 (x2-x1)2=10. ⑥
将④式代入⑥式并整理得(5b2-3a2)2-16a2b4=0. ——10分
将b2=3a2代入上式,得a2=1,将a2=1代入b2=3a2得b2=3.
故所求双曲线方程为x2-
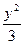 =1. ——12分
=1. ——12分
练习册系列答案
相关题目
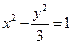 ,双曲线存在关于直线
,双曲线存在关于直线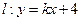 对称的点,求实数
对称的点,求实数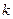 的取值范围。
的取值范围。 与曲线
与曲线 相交于
相交于 两点,则直线
两点,则直线 的倾斜角的范围是( )
的倾斜角的范围是( )



 的焦点为
的焦点为 ,弦
,弦 过
过 且在双曲线的一支上,若
且在双曲线的一支上,若 ,则
,则 等于( )
等于( )


 、
、 ,且经过点
,且经过点 ,则双曲线的标准方程是( )
,则双曲线的标准方程是( )



 充分不必要条件 B
充分不必要条件 B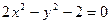 的右焦点作直线
的右焦点作直线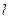 交曲线于A、B两点,若
交曲线于A、B两点,若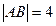 则这样的直线存在 ( )
则这样的直线存在 ( ) 0条 B
0条 B