题目内容
已知椭圆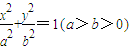
的焦距为2c，且a，b，c依次成等差数列，则椭圆的离心率为 ．
【答案】分析：利用等差数列的性质及a，b，c间的关系建立关于a、c的方程，转化为关于e的方程，求出e的值．
解答：解：∵a，b，c依次成等差数列，∴2b=a+c，又 a2-b2=c2，∴a2-
=c2，
即 3a2-5c2-2ac=0，∴-5e2-2e+3=0，e=
或 e=-1（舍去）．
故答案为：
．
点评：本题考查椭圆的标准方程和简单性质、等差数列的性质的应用，注意离心率的范围．
解答：解：∵a，b，c依次成等差数列，∴2b=a+c，又 a2-b2=c2，∴a2-
=c2，即 3a2-5c2-2ac=0，∴-5e2-2e+3=0，e=
或 e=-1（舍去）．故答案为：
．点评：本题考查椭圆的标准方程和简单性质、等差数列的性质的应用，注意离心率的范围．
练习册系列答案
相关题目
的焦距为2c，左准线为l，长轴顶点为
、
，过椭圆上任意纵坐标非零的点P作直线
与
分别交l于M、N两点
(O为原点)上是否能找到一点Q，使得对于上述的点P，
恒为直角，若能，求出点Q的坐标；若不能说明理由；
时，点B恰为线段RC的中点，求此椭圆的离心率．
的焦距为2c，且a，b，c依次成等差数列，则椭圆的离心率为 ________．