题目内容
已知椭圆![]() 的焦距为2c,左准线为l,长轴顶点为
的焦距为2c,左准线为l,长轴顶点为![]() 、
、![]() ,过椭圆上任意纵坐标非零的点P作直线
,过椭圆上任意纵坐标非零的点P作直线![]() 与
与![]() 分别交l于M、N两点
分别交l于M、N两点![]()
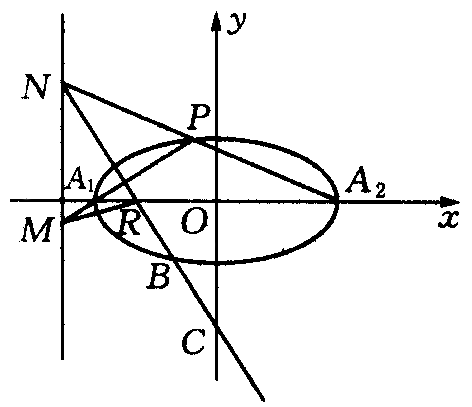
(1)试问在线段![]() (O为原点)上是否能找到一点Q,使得对于上述的点P,
(O为原点)上是否能找到一点Q,使得对于上述的点P,![]() 恒为直角,若能,求出点Q的坐标;若不能说明理由;
恒为直角,若能,求出点Q的坐标;若不能说明理由;
(2)如图,设直线NR与椭圆交于点B,与y轴交于点C,当直线PN的斜率为![]() 时,点B恰为线段RC的中点,求此椭圆的离心率.
时,点B恰为线段RC的中点,求此椭圆的离心率.
答案:
解析:
解析:
|
(2) (1)当点P运动到特殊位置(0,b)时,直线
证明:设椭圆上任意一点
(2)直线
|

练习册系列答案
相关题目
 ,
, 由
由 ,所以直线BN的方程为
,所以直线BN的方程为
 的焦距为2c,且a,b,c依次成等差数列,则椭圆的离心率为 ________.
的焦距为2c,且a,b,c依次成等差数列,则椭圆的离心率为 ________.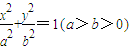 的焦距为2c,且a,b,c依次成等差数列,则椭圆的离心率为 .
的焦距为2c,且a,b,c依次成等差数列,则椭圆的离心率为 .