题目内容
若函数 是R上的单调递增函数,则a的取值范围是________.
是R上的单调递增函数,则a的取值范围是________.

分析:结合函数的图象分析知,函数
 是R上的单调递增函数,必有a>0,1≥a2-1>0三个同时成立,由此可以解出a的取值范围
是R上的单调递增函数,必有a>0,1≥a2-1>0三个同时成立,由此可以解出a的取值范围解答:函数
 是R上的单调递增函数,
是R上的单调递增函数,故有

即
 解得1<a≤
解得1<a≤ ,即a的取值范围是(1,
,即a的取值范围是(1, ]
]故答案为(1,
 ].
].点评:考查分段函数的单调性,函数在R上是增函数,故必有x≤0上的最大值小于x≥0上的最小值,此结论在解题中易被忽略导致错误,解题时需谨记.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 ,则
,则 =
=



 则
则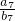 的值为________.
的值为________. ).
).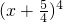 的展开式中x3的系数相等,则锐角θ的值是
的展开式中x3的系数相等,则锐角θ的值是



 ,经过点M(1,1)能否作一条直线l,使直线l与双曲线交于A、B,且M是线段AB的中点,若存在这样的直线l,求出它的方程;若不存在,说明理由.
,经过点M(1,1)能否作一条直线l,使直线l与双曲线交于A、B,且M是线段AB的中点,若存在这样的直线l,求出它的方程;若不存在,说明理由.