题目内容
已知函数fn（x）=x3-nx-1（x＞0，n∈N*）．
（Ⅰ）求函数f3（x）的极值；
（Ⅱ）判断函数fn（x）在区间(
，
)上零点的个数，并给予证明．
（Ⅰ）求函数f3（x）的极值；
（Ⅱ）判断函数fn（x）在区间(
| n |
| n+1 |
（Ⅰ）∵f3(x)=x3-3x-1，∴f3′(x)=3x2-3，
∵当x＞1时，f3′(x)＞0；当0＜x＜1时，f3′(x)＜0．
∴当x=1时，f3（x）取得极小值-3，无极大值；
（Ⅱ）函数fn（x）在区间(
，
)上有且只有一个零点．
证明：
∵fn(
)=(
)3-n
-1=-1＜0，
fn(
)=(
)3-n
-1=
-1＞0，
fn(
)•fn(
)＜0，∴函数fn（x）在区间(
，
)上必定存在零点．
∵fn′(x)=3x2-n，∴当x∈(
，
)时，fn′(x)＞3(
)2-n=2n＞0，
∴fn（x）在区间(
，
)上单调递增，
∴函数fn（x）在区间(
，
)上的零点最多一个．
综上知：函数fn（x）在区间(
，
)上存在唯一零点．
∵当x＞1时，f3′(x)＞0；当0＜x＜1时，f3′(x)＜0．
∴当x=1时，f3（x）取得极小值-3，无极大值；
（Ⅱ）函数fn（x）在区间(
| n |
| n+1 |
证明：
∵fn(
| n |
| n |
| n |
fn(
| n+1 |
| n+1 |
| n+1 |
| n+1 |
fn(
| n |
| n+1 |
| n |
| n+1 |
∵fn′(x)=3x2-n，∴当x∈(
| n |
| n+1 |
| n |
∴fn（x）在区间(
| n |
| n+1 |
∴函数fn（x）在区间(
| n |
| n+1 |
综上知：函数fn（x）在区间(
| n |
| n+1 |
练习册系列答案
核心素养学练评系列答案
相关题目
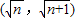上零点的个数，并给予证明．