题目内容
已知函数fn(x)=x3-nx-1(x>0,n∈N*).(Ⅰ)求函数f3(x)的极值;
(Ⅱ)判断函数fn(x)在区间
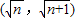 上零点的个数,并给予证明.
上零点的个数,并给予证明.
【答案】分析:(Ⅰ)求出函数f3(x)的导函数,在定义域内根据导函数的符号判断原函数在不同区间内的单调性,由单调性分析极值;
(Ⅱ)由 可知函数fn(x)在区间
可知函数fn(x)在区间 上有零点,然后利用导函数的符号得到函数fn(x)在区间
上有零点,然后利用导函数的符号得到函数fn(x)在区间 上单调递增,从而得到答案.
上单调递增,从而得到答案.
解答:解:(Ⅰ)∵ ,∴
,∴ ,
,
∵当x>1时, ;当0<x<1时,
;当0<x<1时, .
.
∴当x=1时,f3(x)取得极小值-3,无极大值;
(Ⅱ)函数fn(x)在区间 上有且只有一个零点.
上有且只有一个零点.
证明:
∵ ,
,
 ,
,
 ,∴函数fn(x)在区间
,∴函数fn(x)在区间 上必定存在零点.
上必定存在零点.
∵ ,∴当
,∴当 时,
时, ,
,
∴fn(x)在区间 上单调递增,
上单调递增,
∴函数fn(x)在区间 上的零点最多一个.
上的零点最多一个.
综上知:函数fn(x)在区间 上存在唯一零点.
上存在唯一零点.
点评:本题主要考查函数在某点取得极值的条件,考查了零点存在性定理,单调函数在区间[a,b]上满足f(a)f(b)<0,则函数在区间(a,b)上有唯一零点,是中档题.
(Ⅱ)由
 可知函数fn(x)在区间
可知函数fn(x)在区间 上有零点,然后利用导函数的符号得到函数fn(x)在区间
上有零点,然后利用导函数的符号得到函数fn(x)在区间 上单调递增,从而得到答案.
上单调递增,从而得到答案.解答:解:(Ⅰ)∵
 ,∴
,∴ ,
,∵当x>1时,
 ;当0<x<1时,
;当0<x<1时, .
.∴当x=1时,f3(x)取得极小值-3,无极大值;
(Ⅱ)函数fn(x)在区间
 上有且只有一个零点.
上有且只有一个零点.证明:
∵
 ,
, ,
, ,∴函数fn(x)在区间
,∴函数fn(x)在区间 上必定存在零点.
上必定存在零点.∵
 ,∴当
,∴当 时,
时, ,
,∴fn(x)在区间
 上单调递增,
上单调递增,∴函数fn(x)在区间
 上的零点最多一个.
上的零点最多一个.综上知:函数fn(x)在区间
 上存在唯一零点.
上存在唯一零点.点评:本题主要考查函数在某点取得极值的条件,考查了零点存在性定理,单调函数在区间[a,b]上满足f(a)f(b)<0,则函数在区间(a,b)上有唯一零点,是中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目