题目内容
在数列{an}中,a1=1,3anan-1+an-an-1=0(n≥2,n∈N*)。
(1)试判断数列 是否成等差数列;
是否成等差数列;
(2)设{bn}满足bn=anan+1,求数列{bn}的前n项和Sn;
(3)若λan+ ≥λ对任意n≥2的整数恒成立,求实数λ的取值范围。
≥λ对任意n≥2的整数恒成立,求实数λ的取值范围。
(1)试判断数列
 是否成等差数列;
是否成等差数列;(2)设{bn}满足bn=anan+1,求数列{bn}的前n项和Sn;
(3)若λan+
 ≥λ对任意n≥2的整数恒成立,求实数λ的取值范围。
≥λ对任意n≥2的整数恒成立,求实数λ的取值范围。解:(1)由已知可得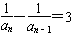 (n≥2)
(n≥2)
故数列{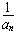 }是等差数列。
}是等差数列。
(2)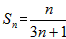 ;
;
(3)将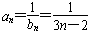 代入
代入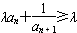 并整理得
并整理得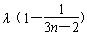 ≤3n+1
≤3n+1
∴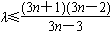
原命题等价于该式对n≥2恒成立
设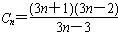
则Cn+1-Cn=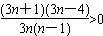 ,Cn+1>Cn
,Cn+1>Cn
∵n=2时,Cn的最小值C2为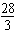
∴λ的取值范围是(-∞,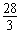 ]。
]。
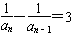 (n≥2)
(n≥2)故数列{
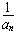 }是等差数列。
}是等差数列。(2)
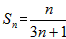 ;
;(3)将
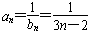 代入
代入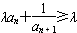 并整理得
并整理得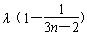 ≤3n+1
≤3n+1∴
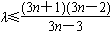
原命题等价于该式对n≥2恒成立
设
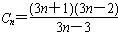
则Cn+1-Cn=
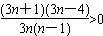 ,Cn+1>Cn
,Cn+1>Cn∵n=2时,Cn的最小值C2为
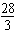
∴λ的取值范围是(-∞,
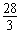 ]。
]。
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.