题目内容
在数列{an}中，a
，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，令bn=
（n∈N*）．（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）设数列{
}的前n项和为Tn，证明：
．
【答案】分析：（Ⅰ）由an•an-1=an-1-an，得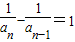
，由此推导出bn-bn-1=1，从而得到bn=n+2．
（Ⅱ）由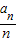
=
=
（
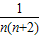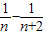），利用错位相减法求出Tn=
[
-（
+
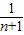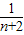）]，由此能够证明
．
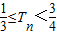解答：（本小题满分14分）
解：（Ⅰ）∵数列{an}中，a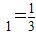
，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，bn=
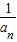（n∈N*），
∴当n=1时，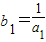
=3；
当n≥2时，由an•an-1=an-1-an，得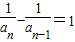
，
∴bn-bn-1=1，
∴数列{bn}是首项为3，公差为1的等差数列，
∴bn=n+2．
（Ⅱ）∵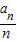
=
=
（
），
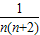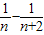∴Tn=
（1-
+
-
+
-
+…+
-
+
-
=
[
-（
+
）]，
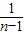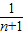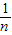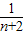
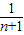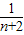∴Tn是关于变量n的增函数，当n趋近无穷大时，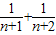
的值趋近于0，
当n=1时，Tn取最小值
，故有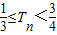
．
点评：本题考查数列的通项公式的求法，考查不等式的证明，解题时要认真审题，注意迭代法和裂顶求和法的合理运用．
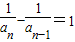，由此推导出bn-bn-1=1，从而得到bn=n+2．（Ⅱ）由
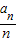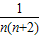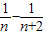==（），利用错位相减法求出Tn=[-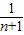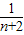（+）]，由此能够证明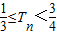．解答：（本小题满分14分）
解：（Ⅰ）∵数列{an}中，a
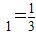，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，bn=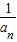（n∈N*），∴当n=1时，
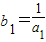=3；当n≥2时，由an•an-1=an-1-an，得
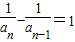，∴bn-bn-1=1，
∴数列{bn}是首项为3，公差为1的等差数列，
∴bn=n+2．
（Ⅱ）∵
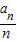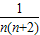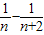==（），∴Tn=
（1-+-+-+…+-+-=
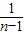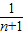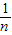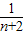
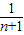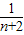[-（+）]，∴Tn是关于变量n的增函数，当n趋近无穷大时，
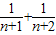的值趋近于0，当n=1时，Tn取最小值
，故有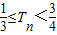．点评：本题考查数列的通项公式的求法，考查不等式的证明，解题时要认真审题，注意迭代法和裂顶求和法的合理运用．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目