题目内容
已知关于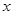 的函数
的函数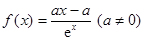
(Ⅰ)当 时,求函数
时,求函数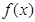 的极值;
的极值;
(Ⅱ)若函数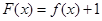 没有零点,求实数
没有零点,求实数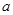 取值范围.
取值范围.
(Ⅰ)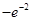 ;(Ⅱ)
;(Ⅱ)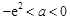
解析试题分析:(Ⅰ)先求导再讨论其单调性,根据单调性可求其极值。(Ⅱ)先求导再讨论函数的单调性,根据单调性求其极值或最值,因为函数没有零点,所以函数的极大值小于0或极小值大于0。否则函数将存在零点。
试题解析:解:(Ⅰ)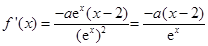 ,
,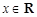 . 2分
. 2分
当 时,
时,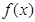 ,
,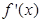 的情况如下表:
的情况如下表: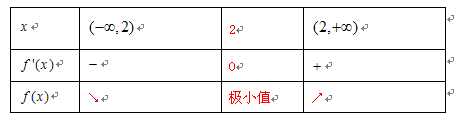
所以,当 时,函数
时,函数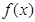 的极小值为
的极小值为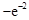 . 6分
. 6分
(Ⅱ)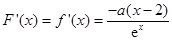 .
.
①当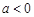 时,
时,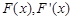 的情况如下表:
的情况如下表:
7分
因为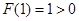 , 8分
, 8分
若使函数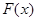 没有零点,需且仅需
没有零点,需且仅需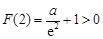 ,解得
,解得 , 9分
, 9分
所以此时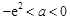 ; 10分
; 10分
②当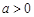 时,
时,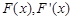 的情况如下表:
的情况如下表: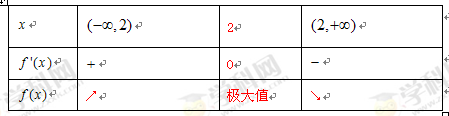 11分
11分
因为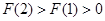 ,且
,且 , 12分
, 12分
所以此时函数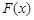 总存在零点. 13分
总存在零点. 13分
综上所述,所求实数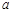 的取值范围是
的取值范围是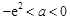 .
.
考点:考查导数和利用导数研究函数性质的方法的数学思想,意在考查考生灵活应用导数分析、解决问题的能力,考查考生的逻辑思维能力、运算能力和创新应用能力。

练习册系列答案
相关题目

 时,求
时,求 的单调区间;
的单调区间; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围. ,其中
,其中 是自然对数的底数,
是自然对数的底数,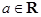 .
. 的单调区间;
的单调区间;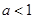 时,试确定函数
时,试确定函数 的零点个数,并说明理由.
的零点个数,并说明理由. ,其中
,其中 .
. ,求
,求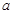 的值,并求此时曲线
的值,并求此时曲线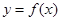 在点
在点 处的切线方程;
处的切线方程;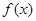 在区间
在区间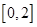 上的最小值.
上的最小值.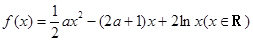 .
.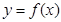 在x=l和x=3处的切线互相平行,求a的值及函数
在x=l和x=3处的切线互相平行,求a的值及函数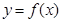 的单调区间;
的单调区间;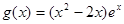 ,若对任意
,若对任意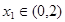 ,均存在
,均存在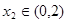 ,使得
,使得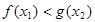 ,求实数a的取值范围.
,求实数a的取值范围.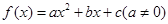 ,曲线
,曲线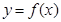 通过点(0,2a+3),且在
通过点(0,2a+3),且在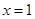 处的切线垂直于y轴.
处的切线垂直于y轴.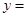 g(x)为偶函数,且当
g(x)为偶函数,且当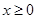 时,
时,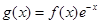 ,求当
,求当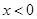 时g(x)的表达式,并求函数g(x)在R上的最小值及相应的x值.
时g(x)的表达式,并求函数g(x)在R上的最小值及相应的x值.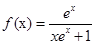 .
.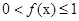 ;
;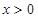 时,
时,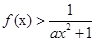 ,求
,求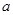 的取值范围.
的取值范围.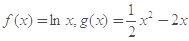 .
.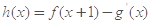 (其中
(其中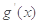 是
是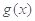 的导函数),求
的导函数),求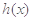 的最大值;
的最大值;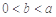 时,有
时,有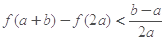 ;
;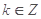 ,当
,当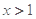 时,不等式
时,不等式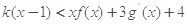 恒成立,求
恒成立,求 的最大值.
的最大值.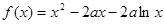 (
(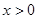 ,
,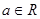 ),
),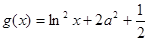 .
.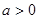 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数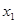 、
、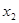 ,均有
,均有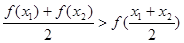 成立;
成立; ,若
,若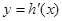 在
在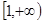 上单调递增,求实数
上单调递增,求实数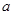 的取值范围;
的取值范围;